题目内容
设点An(xn,0),Pn(xn,2n-1)和抛物线Cn:y=x2+anx+bn(n∈N*),其中an=-2-4n- ,xn由以下方法得到:x1=1,点P2(x2,2)在抛物线C1:y=x2+a1x+b1上,点A1(x1,0)到P2的距离是A1到C1上点的最短距离,…,点Pn+1(xn+1,2n)在抛物线Cn:y=x2+anx+bn上,点An(xn,0)到Pn+1的距离是An到Cn上点的最短距离.
,xn由以下方法得到:x1=1,点P2(x2,2)在抛物线C1:y=x2+a1x+b1上,点A1(x1,0)到P2的距离是A1到C1上点的最短距离,…,点Pn+1(xn+1,2n)在抛物线Cn:y=x2+anx+bn上,点An(xn,0)到Pn+1的距离是An到Cn上点的最短距离.(Ⅰ)求x2及C1的方程.
(Ⅱ)证明{xn}是等差数列.
【答案】分析:本题考查数列与解析几何的综合问题,涉及了抛物线方程、直线与抛物线的关系、导数及其几何意义、求曲线方程、证明等差数列、数学归纳法等多方面的知识和方法.
对于(Ⅰ)的求解,要充分利用点在抛物线上则满足抛物线方程,结合两点间的距离公式用点p(x,y)表示|A1P|,然后借助于导数,利用f'(x2)=0建立方程,最终使问题得到解决.
对于(Ⅱ)类比(Ⅰ),首先利用点P(x,y)是Cn上任意一点,得到|AnP|=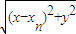 =
=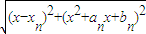 ,然后利用导数思想获得xn+1-xn)+2(xn+12+anx+bn)(2xn+1+an)=0并由此通过数学归纳法证明出xn=2n-1,也即证明了{xn}是等差数列.
,然后利用导数思想获得xn+1-xn)+2(xn+12+anx+bn)(2xn+1+an)=0并由此通过数学归纳法证明出xn=2n-1,也即证明了{xn}是等差数列.
解答:解:(Ⅰ)由题意得A1(1,0),C1:y=x2-7x+b1,
设点P(x,y)是C1上任意一点,
则|A1P|=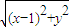 =
=
令f(x)=(x-1)2+(x2-7x+b1)2
则f'(x)=2(x-1)+2(x2-7x+b1)(2x-7)
由题意得f'(x2)=0,
即2(x2-1)+2(x22-7x+b1)(2x2-7)=0
又P2(x2,2)在C1上,∴2=x22-7x2+b1
解得x2=3,b1=14
故C1的方程为y=x2-7x+14
(Ⅱ)设点P(x,y)是Cn上任意一点,
则|AnP|=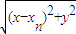 =
=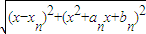
令g(x)=(x-xn)2+(x2+anx+bn)2
则g'(x)=2(x-xn)+2(x2+anx+bn)(2x+an)
由题意得g'(xn+1)=0
即2(xn+1-xn)+2(xn+12+anx+bn)(2xn+1+an)=0
又∵2n=xn+1,∴(xn+1-xn)+2n(2xn+1+an)=0(n≥1),
即(1+2n+1)xn+1-xn+2nan=0??(*)
下面用数学归纳法证明xn=2n-1,
①当n=1时,x1=1,等式成立;
②假设当n=k时,等式成立,即xk=2k-1,
则当n=k+1时,由(*)知(1+2k+1)xk+1-xk+2kak=0,
又ak=2-4k-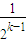 ,∴xk+1=
,∴xk+1=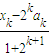 =2k+1,
=2k+1,
即n=k+1时,等式成立.
由①②知,等式对n∈N*成立,
故{xn}是等差数列.
点评:本题的综合性极强,是多种知识和方法的汇总,处理起来难度较大,不仅需要具备综合运用知识的能力,还要运算准确,不走弯路,像这样的题目,在山东省的近几年高考中少见,不是所有人所追求,只提供给部分数学功底强劲的同学研究,希望量力而行.
对于(Ⅰ)的求解,要充分利用点在抛物线上则满足抛物线方程,结合两点间的距离公式用点p(x,y)表示|A1P|,然后借助于导数,利用f'(x2)=0建立方程,最终使问题得到解决.
对于(Ⅱ)类比(Ⅰ),首先利用点P(x,y)是Cn上任意一点,得到|AnP|=
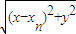 =
=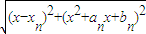 ,然后利用导数思想获得xn+1-xn)+2(xn+12+anx+bn)(2xn+1+an)=0并由此通过数学归纳法证明出xn=2n-1,也即证明了{xn}是等差数列.
,然后利用导数思想获得xn+1-xn)+2(xn+12+anx+bn)(2xn+1+an)=0并由此通过数学归纳法证明出xn=2n-1,也即证明了{xn}是等差数列.解答:解:(Ⅰ)由题意得A1(1,0),C1:y=x2-7x+b1,
设点P(x,y)是C1上任意一点,
则|A1P|=
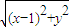 =
=
令f(x)=(x-1)2+(x2-7x+b1)2
则f'(x)=2(x-1)+2(x2-7x+b1)(2x-7)
由题意得f'(x2)=0,
即2(x2-1)+2(x22-7x+b1)(2x2-7)=0
又P2(x2,2)在C1上,∴2=x22-7x2+b1
解得x2=3,b1=14
故C1的方程为y=x2-7x+14
(Ⅱ)设点P(x,y)是Cn上任意一点,
则|AnP|=
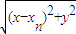 =
=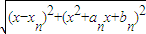
令g(x)=(x-xn)2+(x2+anx+bn)2
则g'(x)=2(x-xn)+2(x2+anx+bn)(2x+an)
由题意得g'(xn+1)=0
即2(xn+1-xn)+2(xn+12+anx+bn)(2xn+1+an)=0
又∵2n=xn+1,∴(xn+1-xn)+2n(2xn+1+an)=0(n≥1),
即(1+2n+1)xn+1-xn+2nan=0??(*)
下面用数学归纳法证明xn=2n-1,
①当n=1时,x1=1,等式成立;
②假设当n=k时,等式成立,即xk=2k-1,
则当n=k+1时,由(*)知(1+2k+1)xk+1-xk+2kak=0,
又ak=2-4k-
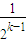 ,∴xk+1=
,∴xk+1=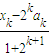 =2k+1,
=2k+1,即n=k+1时,等式成立.
由①②知,等式对n∈N*成立,
故{xn}是等差数列.
点评:本题的综合性极强,是多种知识和方法的汇总,处理起来难度较大,不仅需要具备综合运用知识的能力,还要运算准确,不走弯路,像这样的题目,在山东省的近几年高考中少见,不是所有人所追求,只提供给部分数学功底强劲的同学研究,希望量力而行.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,
如图,