题目内容
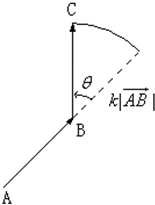 如图,
如图,| BC |
| AB |
| BC |
| AB |
| AB |
| BC |
| OA1 |
(1)向量
| OA1 |
| π |
| 2 |
| 1 |
| 2 |
| A1A2 |
| A2A3 |
| A1A2 |
| A2A3 |
(2)向量
| OA1 |
| π |
| 2 |
| 1 |
| 2 |
为
| An-1An |
| lim |
| n→∞ |
| lim |
| n→∞ |
(3)向量
| OA1 |
| A1A2 |
| A2A3 |
| OA1 |
| A1A2 |
| A2A3 |
分析:(1)向量
经过1次(
,
)延伸,得到向量
所在有向线段正向与y轴正向相同,且模为
,A2(1,
),
=(0,
),类似的,求出
=(-
,0)
(2)
=
+
+…+
,利用向量运算求出表达式,得出xn,yn再求极限.
(3)若
、
、
恰能够构成一个三角形,即
+
+
=
,建立关于的方程组,再解方程组即可.
| OA1 |
| π |
| 2 |
| 1 |
| 2 |
| A1A2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A1A2 |
| 1 |
| 2 |
| A2A3 |
| 1 |
| 4 |
(2)
| OAn |
| OA1 |
| A1A2 |
| An-1An |
(3)若
| OA1 |
| A1A2 |
| A2A3 |
| OA |
| A1A2 |
| A2A3 |
| 0 |
解答: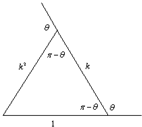 解:(1)
解:(1)
=(0,
),
=(-
,0)
(2)
=(0,-
),
=(
,0),
=(0,
),…
因为
=
+
+…+
所以
xn=1-
+
-
+…=
,
yn=
-
+
-…=
所以,A(
,
)
(3)
=(kcosθ,ksinθ),
=(k2cos2θ,k2sin2θ)
又∵
+
+
=
∴(1+kcosθ+k2cos2θ,ksinθ+k2sin2θ)=(0,0)
∴
解得:k=1,θ=120°
 解:(1)
解:(1)| A1A2 |
| 1 |
| 2 |
| A2A3 |
| 1 |
| 4 |
(2)
| A3A4 |
| 1 |
| 8 |
| A4A5 |
| 1 |
| 16 |
| A5A6 |
| 1 |
| 32 |
因为
| OAn |
| OA1 |
| A1A2 |
| An-1An |
所以
| lim |
| n→∞ |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 64 |
| 4 |
| 5 |
| lim |
| n→∞ |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 32 |
| 2 |
| 5 |
所以,A(
| 4 |
| 5 |
| 2 |
| 5 |
(3)
| A1A2 |
| A2A3 |
又∵
| OA |
| A1A2 |
| A2A3 |
| 0 |
∴(1+kcosθ+k2cos2θ,ksinθ+k2sin2θ)=(0,0)
∴
|
解得:k=1,θ=120°
点评:本题是新定义题目,首先读懂新定义的实质,转化成我们已有的知识并解决.本题实质考查向量的坐标运算,几何运算,极限运算,方程的思想.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
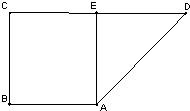
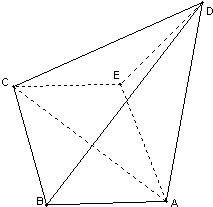
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,E是棱CC1上动点,F是AB中点,AC=BC=2,AA1=4.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,E是棱CC1上动点,F是AB中点,AC=BC=2,AA1=4.