题目内容
7.命题“?x0∈R,x02+x0+2017>0”的否定为( )| A. | ?x0∈R,${x_0}^2+{x_0}+2017<0$ | B. | ?x∈R,x2+x+2017≤0 | ||
| C. | ?x0∈R,${x_0}^2+{x_0}+2017≤0$ | D. | ?x∈R,x2+x+2017>0 |
分析 根据特称命题的否定是全称命题进行判断即可.
解答 解:命题是特称命题,则命题的否定是全称命题,
即命题的否定是:?x∈R,x2+x+2017≤0,
故选:B
点评 本题主要考查含有量词的命题的否定,根据特称命题的否定是全称命题是解决本题的关键.比较基础.

练习册系列答案
相关题目
17. 某几何体三视图如图所示,则该几何体体积为( )
某几何体三视图如图所示,则该几何体体积为( )
 某几何体三视图如图所示,则该几何体体积为( )
某几何体三视图如图所示,则该几何体体积为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
2.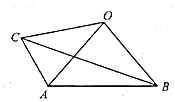 如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )
如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )
 如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )
如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )| A. | $\frac{13}{6}$ | B. | $\frac{8}{3}$ | C. | $\frac{17}{6}$ | D. | $\frac{13}{3}$ |
16.已知集合A={x|$\frac{x-10}{x-1}$≤0},B={y|y=lgx,x∈A},则A∪B=( )
| A. | {1} | B. | ∅ | C. | [0,10] | D. | (0,10] |
17.下列命题中的真命题为( )
| A. | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一的实数λ,使得$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |
| B. | 已知随机变量ξ服从正态分布N(1,σ2),若P(ξ≤4)=0.79,则P(ξ≤-2)=0.21 | |
| C. | “φ=$\frac{3π}{2}$”是“y=sin(2x+φ)为偶函数”的充要条件 | |
| D. | 函数y=f(1+x)与函数y=f(1-x)的图象关于直线x=1对称 |

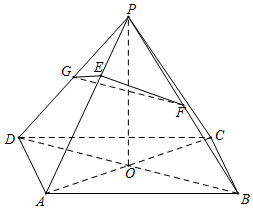 四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠DAB=$\frac{2π}{3}$,AC∩BD=O,且PO⊥平面ABCD,PO=$\sqrt{3}$,点F,G分别是线段PB,PD上的中点,E在PA上,且PA=3PE.
四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠DAB=$\frac{2π}{3}$,AC∩BD=O,且PO⊥平面ABCD,PO=$\sqrt{3}$,点F,G分别是线段PB,PD上的中点,E在PA上,且PA=3PE.