题目内容
在数列 中,已知
中,已知 (
(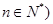 .
.
(Ⅰ)求 及
及 ;
;
(Ⅱ)求数列 的前
的前 项和
项和 .
.
(Ⅰ)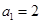 ,
, =2n。
=2n。
(Ⅱ)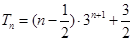 。
。
解析试题分析:(Ⅰ)因为 (
(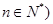 ,
,
所以当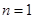 时,
时,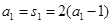 ,解得
,解得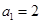 ; (2分)
; (2分)
当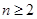 时,
时,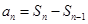
所以 是一个以2为首项,以2为公差的等差数列,
是一个以2为首项,以2为公差的等差数列,
所以 =2n (7分)
=2n (7分)
(Ⅱ)因为 ,数列
,数列 的前
的前 项和
项和 ,
,
所以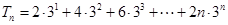 , (8分)
, (8分) , (9分)
, (9分)
两式相减得: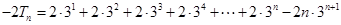 (10分)
(10分)
= 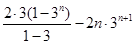
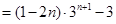 (13分)
(13分)
所以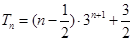 (14分)
(14分)
考点:等差数列的通项公式,“错位相减法”。
点评:中档题,涉及数列的通项公式的确定,往往利用已知条件,建立相关元素的方程组。“分组求和法”“裂项相消法”“错位相减法”是高考常常考查的数列的求和方法。

练习册系列答案
相关题目
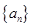 满足
满足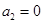 ,
,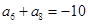 .
.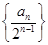 的前n项和.
的前n项和.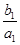 +
+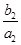 +…+
+…+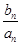 =1-
=1-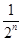 ,n∈N*,求{bn}的前n项和Tn.
,n∈N*,求{bn}的前n项和Tn.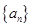 中,点
中,点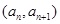
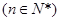 在直线
在直线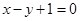 上,且
上,且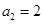 .
. 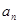 ;
;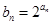 ,数列
,数列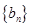 的前
的前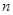 项和为
项和为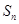 ,
,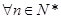 ,
,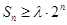 成立,求实数
成立,求实数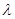 的取值范围.
的取值范围. 中,
中,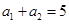 ,
,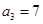 ,记数列
,记数列 的前
的前 项和为
项和为 .
. 、
、 ,使得
,使得 、
、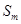 、
、 前3项的和为
前3项的和为 ,前3项的积为8,
,前3项的积为8, ,求数列
,求数列 的前
的前 项和
项和 。
。 为等差数列,
为等差数列, 是等差数列的前
是等差数列的前 项和,已知
项和,已知 ,
, .
. ;(2)
;(2) 为数列
为数列 的前
的前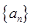 首项为1,且
首项为1,且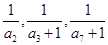 成等比数列,
成等比数列,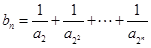
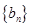 通项公式;
通项公式;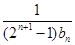 前n项和
前n项和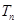 ;
;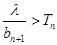 成立,求
成立,求 范围.
范围. 是等差数列,且
是等差数列,且
 项的和
项的和
 ,求
,求 的前
的前