题目内容
各项均为正数的等差数列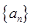 首项为1,且
首项为1,且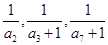 成等比数列,
成等比数列,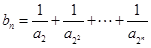
(1)求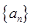 、
、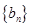 通项公式;
通项公式;
(2)求数列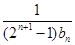 前n项和
前n项和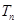 ;
;
(3)若对任意正整数n都有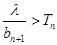 成立,求
成立,求 范围.
范围.
(1)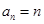
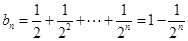 ;
;
(2)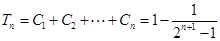 ;
;
(3)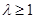 。
。
解析试题分析:(1)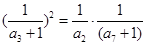 ∴
∴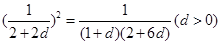
∴公差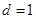
∴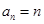
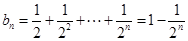 4分
4分
(2)
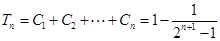 9分;
9分;
(3)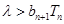 (
( ) ∴
) ∴ 对
对 恒成立
恒成立
又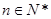 时
时 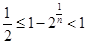 ∴
∴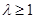 14分
14分
考点:等差数列、等比数列的通项公式,裂项相消法,不等式恒成立问题。
点评:中档题,本题(I)(II)是数列的基本问题, “分组求和法”“裂项相消法”“错位相减法”等,是常常考查的数列求和方法。涉及数列不等式恒成立问题,往往先求和、后放缩、再确定参数的范围。

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 中,已知
中,已知 (
(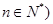 .
. 及
及 ;
; 的前
的前 项和
项和 .
. 的前
的前 项和
项和 (
( ,求证:数列
,求证:数列 是等差数列,并求数列
是等差数列,并求数列 ,
, ,求使得
,求使得 成立的最小正整数
成立的最小正整数 }的前n项和
}的前n项和 ,数列{
,数列{ }满足
}满足 .
. ,数列
,数列 的前
的前 项和为
项和为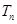 ,求满足
,求满足 的
的 中,
中, ,公差
,公差 为整数,若
为整数,若 ,
, .
. 项和
项和 的最大值;
的最大值;  为等差数列,
为等差数列, 为数列
为数列 项和,已知
项和,已知 .
.  ,求数列
,求数列 的前
的前 .
. ,
, 、
、 、
、 是平面直角坐标系上的三点,且
是平面直角坐标系上的三点,且 、
、 、
、 成等差数列,公差为
成等差数列,公差为 ,
, .
. ,
,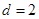 ,点
,点 上时,求点
上时,求点 的方程是
的方程是
 ,过点
,过点 的直线交圆于
的直线交圆于 两点,
两点, 是圆
是圆 上,点
上,点 ,求证:线段
,求证:线段 的垂直平分线与
的垂直平分线与 轴的交点为一定点,并求该定点的坐标.
轴的交点为一定点,并求该定点的坐标. 中,
中, ,不等式
,不等式
 对任意
对任意 都成立.
都成立. 的取值范围;
的取值范围; ,
, ,求证:对任意的
,求证:对任意的 .
.