题目内容
18.若圆(x-1)2+(y+1)2=16上的点P到直线4x+3y=11的距离等于2,点P的个数是( )| A. | 只有一个 | B. | 两个 | C. | 有三个 | D. | 四个 |
分析 求出圆心到直线的距离,进而可得满足条件的P点的个数.
解答 解:圆(x-1)2+(y+1)2=16的圆心(1,-1)到直线4x+3y=11的距离d=$\frac{|4-3-11|}{5}$=2,
圆(x-1)2+(y+1)2=16的半径为4,
故圆上的点P到直线4x+3y=11的距离等于2的个数有3个,
故选:C.
点评 本题考查的知识点是直线与圆的位置关系,点到直线的距离公式,难度中档.

练习册系列答案
相关题目
9.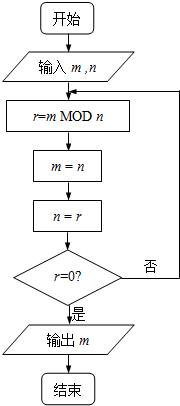 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=( )
 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=( )| A. | 0 | B. | 5 | C. | 45 | D. | 90 |
3.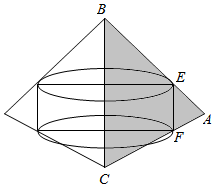 △ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )
△ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )
 △ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )
△ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )| A. | V1>V2 | B. | V1<V2 | ||
| C. | V1=V2 | D. | V1,V2大小关系不确定 |
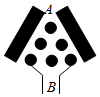 将一个半径适当的小球从如图所示的A入口处,向下自由下落.小球在下落的过程中,将3次遇到黑色障碍物,每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$,最后通过黑色区域.
将一个半径适当的小球从如图所示的A入口处,向下自由下落.小球在下落的过程中,将3次遇到黑色障碍物,每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$,最后通过黑色区域.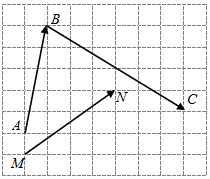 向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{MN}$在正方形网格中的位置如图所示,若$\overrightarrow{MN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$(λ,μ∈R),则$\frac{λ}{μ}$=2.
向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{MN}$在正方形网格中的位置如图所示,若$\overrightarrow{MN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$(λ,μ∈R),则$\frac{λ}{μ}$=2.