题目内容
4．已知角α终边过直线l1：x-y=0和直线l2：2x+y-3=0的交点P．求sinα，cosα，tanα的值．
分析 求出P的坐标，可得r，即可求出sinα，cosα，tanα．
解答 解：由$\left\{\begin{array}{l}{x-y=0}\\{2x+y-3=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$--------------------------------------------（3分）
∴P（1，1）--------------------------------------------------------------（4分）
∴r=$\sqrt{2}$，---------------------------------------------------------（6分）
∴sinα=cosα=$\frac{\sqrt{2}}{2}$，tanα=1．--------------------------------------（12分）
点评 本题考查三角函数的定义，考查两条直线的位置关系，比较基础．
练习册系列答案
相关题目
14．下列选项中，说法正确的是（ ）
| A． | 命题“?x0∈R，${x_0}^2-{x_0}≤0$”的否定为“?x∈R，x2-x＞0” | |
| B． | 命题“在△ABC中，A＞30°，则$sinA＞\frac{1}{2}$”的逆否命题为真命题 | |
| C． | 若非零向量$\overrightarrow a$、$\overrightarrow b$满足$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|-|{\overrightarrow b}|$，则$\overrightarrow a$与$\overrightarrow b$共线 | |
| D． | 设{an}是公比为q的等比数列，则“q＞1”是“{an}为递增数列”的充分必要条件 |
12．设集合A={1，2，3，5}，B={2，4，6}，则A∩B=（ ）
| A． | {2} | B． | {4，6} | C． | {1，3，5} | D． | {4，6，7，8} |
19．若m，n满足m+n-1=0，则直线mx+y+n=0过定点（ ）
| A． | （1，-1） | B． | （0，-n） | C． | （0，0） | D． | （-1，1） |
9．已知角α的终边过点P（-3m，4m）（m＜0），则2sinα+cosα的值是（ ）
| A． | 1 | B． | $\frac{2}{5}$ | C． | -$\frac{2}{5}$ | D． | -1 |
13．为了得到函数=4sin（2x+$\frac{π}{5}$），x∈R的图象，只需把函数y=4sin（x+$\frac{π}{5}$），x∈R的图象上所有点的（ ）
| A． | 横坐标伸长到原来的2倍，纵坐标不变 | |
| B． | 纵坐标伸长到原来的2倍，横坐标不变 | |
| C． | 横坐标缩短到原来的$\frac{1}{2}$倍，纵坐标不变 | |
| D． | 纵坐标缩短到原来的$\frac{1}{2}$倍，横坐标不变 |
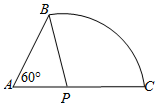某柱体实心铜制零件的截面边长是长度为55毫米线段AB和88毫米的线段AC以及圆心为P，半径为PB的一段圆弧BC构成，其中∠BAC=60°．