题目内容
16.已知函数$y=sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,则( )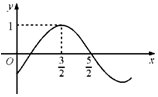
| A. | $ω=\frac{π}{2},φ=-\frac{π}{4}$ | B. | ω=$\frac{π}{2},φ=\frac{π}{4}$ | C. | $ω=π,φ=-\frac{π}{4}$ | D. | $ω=π,φ=\frac{π}{4}$ |
分析 根据图象求出周期,从而求出ω的值,根据f($\frac{3}{2}$)=1,求出φ的值即可.
解答 解:结合图象$\frac{5}{2}$-$\frac{3}{2}$=1,是$\frac{1}{4}$个周期,
故T=4,
故ω=$\frac{2π}{4}$=$\frac{π}{2}$,
而y=sin($\frac{π}{2}$×$\frac{3}{2}$+φ)=1,解得:φ=-$\frac{π}{4}$,
故选:A.
点评 本题给出y=Asin(ωx+φ)的部分图象,求函数的表达式.着重考查了三角函数的图象与性质、函数y=Asin(ωx+φ)的图象变换等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知$f(x)=\left\{\begin{array}{l}(4-a)x\;,\;\;x∈(-∞\;,\;1]\\{a^x}\;,\;\;\;x∈(1\;,\;+∞)\end{array}\right.$是R上的增函数,那么实数a的取值范围是( )
| A. | (1,4) | B. | [1,4) | C. | (2,4) | D. | [2,4) |
4.二次函数f(x)=ax2+bx+1的最小值为f(1)=0,则a-b=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 3 |
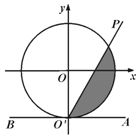 如图,在平面直角坐标系xOy中,单位圆O与y轴负半轴交于点O',过点O'作与x轴平行的直线AB,射线O'P从O'A出发,绕着点O'逆时针方向旋转至O'B,在旋转的过程中,记∠AO'P=x(0<x<π),O'P所经过的在单位圆O内区域(阴影部分)的面积为S.
如图,在平面直角坐标系xOy中,单位圆O与y轴负半轴交于点O',过点O'作与x轴平行的直线AB,射线O'P从O'A出发,绕着点O'逆时针方向旋转至O'B,在旋转的过程中,记∠AO'P=x(0<x<π),O'P所经过的在单位圆O内区域(阴影部分)的面积为S.