题目内容
已知抛物线的顶点在原点,焦点在x轴上,其准线过双曲线
-
=1(a>0,b>0)的一个焦点;又抛物线与双曲线的一个交点为M(
,-
),求抛物线和双曲线的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 6 |
考点:双曲线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:首先根据抛物线的准线过双曲线的焦点,可得p=2c,再利用抛物线与双曲线同过交点(
,-
),求出c、p的值,进而结合双曲线的性质a2+b2=c2,求解即可.
| 3 |
| 2 |
| 6 |
解答:
解:由题设知,抛物线以双曲线的右焦点为焦点,准线过双曲线的左焦点,∴p=2c.
设抛物线方程为y2=4c•x,
∵抛物线过点(
,-
),∴6=4c•
.
∴c=1,故抛物线方程为y2=4x.
又双曲线
-
=1过点(
,-
),
∴
-
=1.①
又a2+b2=c2=1.②
由①②可得a2=
或a2=9(舍).
∴b2=
,
故双曲线方程为:4x2-
=1.
设抛物线方程为y2=4c•x,
∵抛物线过点(
| 3 |
| 2 |
| 6 |
| 3 |
| 2 |
∴c=1,故抛物线方程为y2=4x.
又双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 6 |
∴
| 9 |
| 4a2 |
| 6 |
| b2 |
又a2+b2=c2=1.②
由①②可得a2=
| 1 |
| 4 |
∴b2=
| 3 |
| 4 |
故双曲线方程为:4x2-
| 4y2 |
| 3 |
点评:本题考查了抛物线和双曲线方程的求法:待定系数法,熟练掌握圆锥曲线的性质是解题的关键,同时考查了学生的基本运算能力与运算技巧.

练习册系列答案
相关题目
函数f(x)=
,若f′(x0)=
,则x0等于( )
| x |
| 1 |
| 2 |
| A、-1 | B、1 | C、2 | D、-2 |
| 29π |
| 6 |
| A、第一象限角 |
| B、第二象限角 |
| C、第三象限角 |
| D、第四象限角 |
若直线l1,l2的方向向量分别为
=(2,4,-4),
=(-6,9,6),则( )
| a |
| b |
| A、l1∥l2 |
| B、l1⊥l2 |
| C、l1与l2相交但不垂直 |
| D、以上均不正确 |
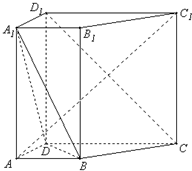 如图,在直四棱柱ANCD-A1B1C1D1中,已知DC=DD1=2AD=2AB=2,AD⊥DC,AB∥DC.
如图,在直四棱柱ANCD-A1B1C1D1中,已知DC=DD1=2AD=2AB=2,AD⊥DC,AB∥DC.