题目内容
14.已知函数$f(x)=\left\{\begin{array}{l}|{ln({-x})}|,x<0\\{x^2}-4x+3,x≥0\end{array}\right.$,若H(x)=f2(x)-2bf(x)+3有8个不同的零点,则实数b的取值范围为($\sqrt{3}$,2].分析 作函数$f(x)=\left\{\begin{array}{l}|{ln({-x})}|,x<0\\{x^2}-4x+3,x≥0\end{array}\right.$的图象,从而可化为x2-2bx+3=0在(0,3]上有两个不同的解;而m(x)=$\frac{x}{2}$+$\frac{3}{2x}$在(0,$\sqrt{3}$)上是减函数,在( $\sqrt{3}$,3]上是增函数;从而解得.
解答 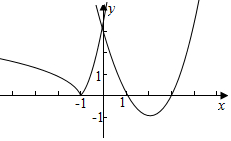 解:作函数$f(x)=\left\{\begin{array}{l}|{ln({-x})}|,x<0\\{x^2}-4x+3,x≥0\end{array}\right.$的图象如下,
解:作函数$f(x)=\left\{\begin{array}{l}|{ln({-x})}|,x<0\\{x^2}-4x+3,x≥0\end{array}\right.$的图象如下,
,∵H(x)=[f(x)]2-2bf(x)+3有8个不同的零点,
∴g(x)=x2-2bx+3在(0,3]上有两个零点;
即x2-2bx+3=0在(0,3]上有两个不同的解;
故b=$\frac{{x}^{2}+3}{2x}$=$\frac{x}{2}$+$\frac{3}{2x}$在(0,3]上有两个不同的解;
而m(x)=$\frac{x}{2}$+$\frac{3}{2x}$在(0,$\sqrt{3}$)上是减函数,在($\sqrt{3}$,3]上是增函数;
而m($\sqrt{3}$)=$\sqrt{3}$,m(3)=2;
故$\sqrt{3}$<b≤2,
故答案为:($\sqrt{3}$,2].
点评 本题考查了分类讨论的思想应用及数形结合的思想应用,同时考查了函数的零点与方程的根的关系应用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
4.sin20°sin10°-cos10°sin70°=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
2.如图是某四棱锥的三视图,则该几何体的表面积等于( )
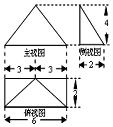

| A. | 34+6$\sqrt{5}$ | B. | 44+12$\sqrt{5}$ | C. | 34+6$\sqrt{3}$ | D. | 32+6$\sqrt{5}$ |
6.设函数f(x)=$\frac{1}{3}$x-lnx(x>0),则函数f(x)( )
| A. | 在区间(0,1)内有零点,在区间(1,+∞)内无零点 | |
| B. | 在区间(0,1)内有零点,在区间(1,+∞)内有零点 | |
| C. | 在区间(0,3),(3,+∞)均无零点 | |
| D. | 在区间(0,3),(3,+∞)均有零点 |
4.已知α,β,γ是三个不同的平面,l1,l2是两条不同的直线,下列命题是真命题的是( )
| A. | 若α⊥γ,β⊥γ,则α∥β | B. | 若l1∥α,l1⊥β,则α∥β | ||
| C. | 若α∥β,l1∥α,l2∥β,则l1∥l2 | D. | 若α⊥β,l1⊥α,l2⊥β,则l1⊥l2 |