题目内容
设函数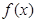 =
=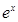 (
(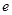 为自然对数的底数),
为自然对数的底数),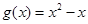 ,记
,记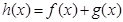 .
.
(1)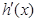 为
为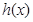 的导函数,判断函数
的导函数,判断函数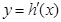 的单调性,并加以证明;
的单调性,并加以证明;
(2)若函数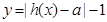 =0有两个零点,求实数
=0有两个零点,求实数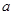 的取值范围.
的取值范围.
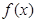 =
=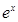 (
(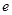 为自然对数的底数),
为自然对数的底数),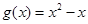 ,记
,记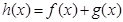 .
.(1)
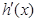 为
为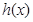 的导函数,判断函数
的导函数,判断函数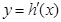 的单调性,并加以证明;
的单调性,并加以证明;(2)若函数
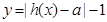 =0有两个零点,求实数
=0有两个零点,求实数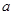 的取值范围.
的取值范围.(1)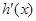 在
在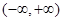 上单调递增.(2)实数a的取值范围是(0,2)。
上单调递增.(2)实数a的取值范围是(0,2)。
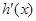 在
在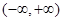 上单调递增.(2)实数a的取值范围是(0,2)。
上单调递增.(2)实数a的取值范围是(0,2)。试题分析:(1)
 ,∴
,∴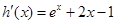 ,
,令
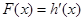 ,则
,则 ,
,∴
 在
在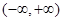 上单调递增,即
上单调递增,即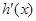 在
在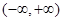 上单调递增.
上单调递增.(2)由(1)知
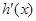 在
在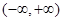 上单调递增,而
上单调递增,而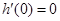 ,
,∴
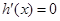 有唯一解
有唯一解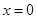 ,
,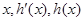 的变化情况如下表所示:
的变化情况如下表所示:| x | 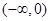 | 0 | 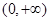 |
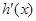 | - | 0 | + |
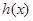 | 递减 | 极小值 | 递增 |
又∵函数
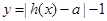 有两个零点,
有两个零点,∴方程
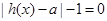 有两个根,即方程
有两个根,即方程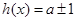 有两个根
有两个根 而
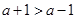 ,
,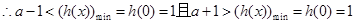 ,
,解得
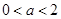 .
.所以,若函数
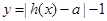 有两个零点,实数a的取值范围是(0,2)
有两个零点,实数a的取值范围是(0,2)点评:中档题,利用导数研究函数单调区间,进一步判断函数零点情况,提供了解答此类问题的一般方法。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
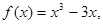
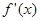 ;
;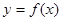 的切线方程。
的切线方程。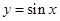 的导函数为( )
的导函数为( )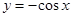
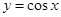
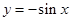
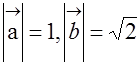 。
。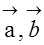 的夹角为
的夹角为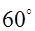 ,求
,求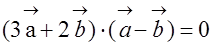 ,求
,求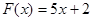 (
(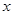 单位为
单位为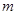 ,
,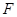 单位为
单位为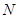 )的作用下,沿着与力
)的作用下,沿着与力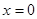 处运动到
处运动到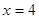 处,则力
处,则力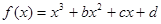 的大致图象,则
的大致图象,则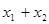 = ( )
= ( )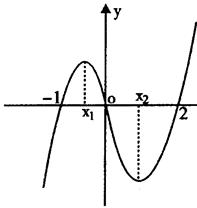
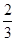
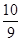
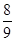
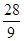
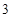
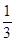
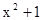 在(1,2)处的切线斜率为( )
在(1,2)处的切线斜率为( )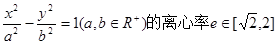 ,则一条渐近线与实轴所构成的角的取值范围是 .
,则一条渐近线与实轴所构成的角的取值范围是 .