题目内容
设函数f(x)是连续函数,且在x=1处存在导数.如函数f(x)及其导函数f′(x)满足f′(x)•lnx=x-
,则函数f(x)( )
| f(x) |
| x |
| A、既有极大值,又有极小值 |
| B、有极大值,无极小值 |
| C、有极小值,无极大值 |
| D、既没有极大值,又没有极小值 |
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:由f′(x)•lnx=x-
,由于(f(x)lnx)′=f′(x)lnx+
,可得f(x)=
,当x≠1时,f′(x)=
.令g(x)=2x2lnx-x2+1,可得g′(x)=4xlnx.利用其单调性可得:当x=1时,g(x)取得极小值即最小值,g(1)=0.进而得出函数f(x)的单调性.
| f(x) |
| x |
| f(x) |
| x |
|
| 2x2lnx-(x2-1) |
| 2xln2x |
解答:
解:由f′(x)•lnx=x-
,∵(f(x)lnx)′=f′(x)lnx+
,
∴(f(x)lnx)′=x,
∴f(x)lnx=
x2+c,(*)
∵函数f(x)是连续函数,
∴由f′(x)•lnx=x-
,可得f(1)=1,
代入(*),可得c=-
.
∴f(x)=
,
当x≠1时,f′(x)=
.
令g(x)=2x2lnx-x2+1,∴g′(x)=4xlnx.
当x>1时,g′(x)>0,g(x)单调递增;当0<x<1时,g′(x)<0,g(x)单调递减法.
∴当x=1时,g(x)取得极小值即最小值,g(1)=0.
∴f′(x)>0(x≠1),且在x=1处存在导数f′(1)=0.
∴函数f(x)在x>0时单调递增.
∴f(x)既没有极大值,又没有最小值.
故选:D.
| f(x) |
| x |
| f(x) |
| x |
∴(f(x)lnx)′=x,
∴f(x)lnx=
| 1 |
| 2 |
∵函数f(x)是连续函数,
∴由f′(x)•lnx=x-
| f(x) |
| x |
代入(*),可得c=-
| 1 |
| 2 |
∴f(x)=
|
当x≠1时,f′(x)=
| 2x2lnx-(x2-1) |
| 2xln2x |
令g(x)=2x2lnx-x2+1,∴g′(x)=4xlnx.
当x>1时,g′(x)>0,g(x)单调递增;当0<x<1时,g′(x)<0,g(x)单调递减法.
∴当x=1时,g(x)取得极小值即最小值,g(1)=0.
∴f′(x)>0(x≠1),且在x=1处存在导数f′(1)=0.
∴函数f(x)在x>0时单调递增.
∴f(x)既没有极大值,又没有最小值.
故选:D.
点评:本题考查了构造函数法利用导数求函数的解析式、利用导数研究函数的单调性极值与最值,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
三个数a=70.3,b=0.37,c=ln0.3的大小关系是( )
| A、a>c>b |
| B、a>b>c |
| C、b>a>c |
| D、c>a>b |
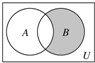 已知全集U=N,A={0,1,2},B={y|y=2x,x∈A},则图中的阴影部分所表示的集合等于( )
已知全集U=N,A={0,1,2},B={y|y=2x,x∈A},则图中的阴影部分所表示的集合等于( )| A、{0} | B、{2} |
| C、{4} | D、{2,4} |
函数f(x)=x-4+log2x的零点所在的区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
若x0是方程式lgx+x=2的解,则x0属于区间( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
函数f(x)=x5-x-1在下列区间一定有零点的是( )
| A、[0,1] |
| B、[1,2] |
| C、[2,3] |
| D、[3,4] |