题目内容
16.已知m,n是空间中两条不同的直线,α、β是两个不同的平面,且m?α,n?β.有下列命题:①若α∥β,则m∥n;
②若α∥β,则m∥β;
③若α∩β=l,且m⊥l,n⊥l,则α⊥β;
④若α∩β=l,且m⊥l,m⊥n,则α⊥β.
其中真命题的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据空间直线和平面,平面和平面平行或垂直的判定定理,分别判断,即可得出结论.
解答 解:①若α∥β,则m∥n或m,n异面,不正确;
②若α∥β,根据平面与平面平行的性质,可得m∥β,正确;
③若α∩β=l,且m⊥l,n⊥l,则α与β不一定垂直,不正确;
④若α∩β=l,且m⊥l,m⊥n,l与n相交则α⊥β,不正确.
故选:B.
点评 本题主要考查命题的真假判断,涉及空间直线和平面,平面和平面平行或垂直的判定,根据相应的判定定理和性质定理是解决本题的关键.

练习册系列答案
相关题目
6.已知集合A={x|x2-3x+2=0},集合B={x|logx4=2},则A∪B=( )
| A. | {-2,1,2} | B. | {-2,2} | C. | {1,2} | D. | {2} |
7.某几何体的三视图如图所示,则该几何体的体积是( )


| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
4.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$,且|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\frac{1}{2}$,则$\overrightarrow{a}$+2$\overrightarrow{b}$与$\overrightarrow{b}$的夹角是( )
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{3π}{4}$ |
5.已知z是复数,且$\frac{z+2}{i}$=1+i,则z在复平面内对应的点的坐标为( )
| A. | (-3,1) | B. | (-3,-1) | C. | (1,-3) | D. | (-1,-3) |
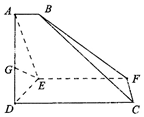 如图,已知梯形CDEF与△ADE所在平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9.CD=12,连接BC,BF.
如图,已知梯形CDEF与△ADE所在平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9.CD=12,连接BC,BF.