题目内容
在等比数列{an}中,S3=
,S6=
,求an.
| 13 |
| 9 |
| 364 |
| 9 |
考点:等比数列的前n项和,等比数列的通项公式
专题:等差数列与等比数列
分析:由已知条件利用等比数列的前n项和公式,列出方程组,求出等比数列的首项和公式,由此能求出an.
解答:
解:∵在等比数列{an}中,S3=
,S6=
,
∴
,
解得a1=
,q=3,
∴an=
•3n-1.
| 13 |
| 9 |
| 364 |
| 9 |
∴
|
解得a1=
| 1 |
| 6 |
∴an=
| 1 |
| 6 |
点评:本题考查等比数列的通项公式的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知全集U=R,集合A={x|x2-x-6≤0},B={x|
>0},那么集合A∩(∁UB)=( )
| x-4 |
| x |
| A、{x|-2≤x<4} |
| B、{x|x≤3或x≥4} |
| C、{x|-2≤x≤0} |
| D、{x|0≤x≤3} |
已知双曲线C:
-
=1的焦距为10,渐近线方程为y=2x,则C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=2esinx在点x=0处的瞬时变化率为( )
| A、2 | B、-2 | C、2e | D、-2e |
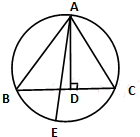
 如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.