��Ŀ����
�ִ����д��������ʽ���֣��籱����·�������Ƕ������ϱ������������ij����У�����˵�������ľ�����������ָ������ֱ�߾��루λ�ƣ�������ʵ��·�̣���ͼ1������ֱ������ƽ���ڣ����Ƕ���A��x1��y1����B��x2��y2�������ġ�ֱ�Ǿ��롱Ϊ��D��AB��=|x1-x2|+|y1-y2|��
��1����ƽ��ֱ������ϵ����ͼ2��д���������㵽ԭ��ġ�ֱ�Ǿ��롱Ϊ2�ġ���㡱�����꣮�����ָ�ᡢ�������Ϊ�����ĵ㣩
��2����������F1��F2�ġ�ֱ�Ǿ��롱��Ϊ��ֵ2a��a��0���Ķ���켣���̣�����ֱ������ϵ�������ö���Ĺ켣
��F1��-1��0����F2��1��0����a=2
��F1��-1��-1����F2��1��1����a=2��
��F1��-1��-1����F2��1��1����a=4��
��3��д��ͬʱ�����������������ġ���㡱�����꣬��˵�����ɣ����ָ�ᡢ�������Ϊ�����ĵ㣩��
�ٵ�A��-1��-1����B��1��1�����㡰ֱ�Ǿ��롱��ȣ�
�ڵ�C��-2��-2����D��2��2�����㡰ֱ�Ǿ��롱����С��
��1����ƽ��ֱ������ϵ����ͼ2��д���������㵽ԭ��ġ�ֱ�Ǿ��롱Ϊ2�ġ���㡱�����꣮�����ָ�ᡢ�������Ϊ�����ĵ㣩
��2����������F1��F2�ġ�ֱ�Ǿ��롱��Ϊ��ֵ2a��a��0���Ķ���켣���̣�����ֱ������ϵ�������ö���Ĺ켣
��F1��-1��0����F2��1��0����a=2

��F1��-1��-1����F2��1��1����a=2��
��F1��-1��-1����F2��1��1����a=4��
��3��д��ͬʱ�����������������ġ���㡱�����꣬��˵�����ɣ����ָ�ᡢ�������Ϊ�����ĵ㣩��
�ٵ�A��-1��-1����B��1��1�����㡰ֱ�Ǿ��롱��ȣ�
�ڵ�C��-2��-2����D��2��2�����㡰ֱ�Ǿ��롱����С��

���㣺�����ľ��빫ʽ
ר�⣺ֱ����Բ
��������1������֪�������ͼ��������������㵽ԭ��ġ�ֱ�Ǿ��롱Ϊ2�ġ���㡱�����꣮
��2�������ٹ켣����Ϊ|x+1|+|x-1|+2|y|=4�������ڹ켣����Ϊ��|x+1|+|y+1|+|x-1|+|y-1|=4�������ۣ��켣����Ϊ��|x+1|+|y+1|+|x-1|+|y-1|=8���ɴ�����������
��3�����������ĸ���У�-2��2������-1��2������-2��1������-1��1������0��0������1��-1������2��-1������1��-2������2��-2�������ڢ٣�����|x+1|+|y+1|=|x-1|+|y-1|���Ӷ�p��{��x��y��|x+y=0��-1��x��1��x��-1��y��1��x��1��y��-1}�����ڢڣ�D��PA��+D��PB��=|x+2|+|y+2|+|x-2|+|y-2|��|x+2+2-x|+|y+2+2-y|=8���Ӷ���P��{��x��y��|-2��x��2��-2��y��2}���ɴ�������������꣮
��2�������ٹ켣����Ϊ|x+1|+|x-1|+2|y|=4�������ڹ켣����Ϊ��|x+1|+|y+1|+|x-1|+|y-1|=4�������ۣ��켣����Ϊ��|x+1|+|y+1|+|x-1|+|y-1|=8���ɴ�����������
��3�����������ĸ���У�-2��2������-1��2������-2��1������-1��1������0��0������1��-1������2��-1������1��-2������2��-2�������ڢ٣�����|x+1|+|y+1|=|x-1|+|y-1|���Ӷ�p��{��x��y��|x+y=0��-1��x��1��x��-1��y��1��x��1��y��-1}�����ڢڣ�D��PA��+D��PB��=|x+2|+|y+2|+|x-2|+|y-2|��|x+2+2-x|+|y+2+2-y|=8���Ӷ���P��{��x��y��|-2��x��2��-2��y��2}���ɴ�������������꣮
���
�⣺��1����ƽ��ֱ������ϵ����ͼ2��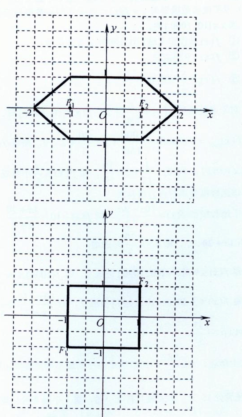
�������㵽ԭ��ġ�ֱ�Ǿ��롱Ϊ2�ġ���㡱�������У�
��0��2��������1��1������2��0������1��-1����
��0��-2������-1��-1������-2��0������-1��1����
��2�������ٹ켣����Ϊ|x+1|+|x-1|+2|y|=4��
��x��-1��y��0ʱ��x-y+2=0��
��x��-1��y��0ʱ��x+y+2=0��
��-1��x��1��y��0ʱ��y=1��
��-1��x��1��y��0ʱ��y=-1��
��x��1��y��0ʱ��x+y-2=0��
��x��1��y��0ʱ��x-y-2=0��
�����ڹ켣����Ϊ��
|x+1|+|y+1|+|x-1|+|y-1|=4��
��x��-1��y��1ʱ����x��y��=��-1��1����
��x��-1��-1��y��1ʱ��x=-1��
��-1��x��1��y��1ʱ��y=1��
�ɶԳ��Կɵ���������ͼ�Σ�
�����ۣ��켣����Ϊ��
|x+1|+|y+1|+|x-1|+|y-1|=8��
��x��-1��y��1ʱ��x-y+3=0��
��x��-1��-1��y��1ʱ��x+3=0��
��-1��x��1��y��1ʱ��y=3��
�ɶԳ��Կɵ���������ͼ�Σ�
��3����ͼ�����������ĸ���У�-2��2������-1��2����
��-2��1������-1��1������0��0������1��-1����
��2��-1������1��-2������2��-2����
���ڢ٣���P��x��y�����㵽A��-1��-1����B��1��1������
��ֱ�Ǿ��롱��ȣ�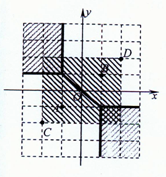
������|x+1|+|y+1|=|x-1|+|y-1|��
���p��{��x��y��|x+y=0��-1��x��1��x��-1��y��1��x��1��y��-1}����ͼ��
���ڢڣ���P��x��y����C��-2��-2����D��2��2�����㡰ֱ�Ǿ��롱����С��
��D��PA��+D��PB��=|x+2|+|y+2|+|x-2|+|y-2|
=|x+2|+|x-2|+|y+2|+|y-2|
��|x+2+2-x|+|y+2+2-y|=8��
���ҽ���-2��x��2��-2��y��2�Ⱥų�����
�ɵõ�P��{��x��y��|-2��x��2��-2��y��2}����ͼ
��ͬʱ���������٢ڵĸ��������ǣ�
��-2��2������-1��2������-2��1������-1��1������0��0����
��1��-1������2��-1������1��-2������2��-2����

�������㵽ԭ��ġ�ֱ�Ǿ��롱Ϊ2�ġ���㡱�������У�
��0��2��������1��1������2��0������1��-1����
��0��-2������-1��-1������-2��0������-1��1����
��2�������ٹ켣����Ϊ|x+1|+|x-1|+2|y|=4��
��x��-1��y��0ʱ��x-y+2=0��
��x��-1��y��0ʱ��x+y+2=0��
��-1��x��1��y��0ʱ��y=1��
��-1��x��1��y��0ʱ��y=-1��
��x��1��y��0ʱ��x+y-2=0��
��x��1��y��0ʱ��x-y-2=0��
�����ڹ켣����Ϊ��
|x+1|+|y+1|+|x-1|+|y-1|=4��
��x��-1��y��1ʱ����x��y��=��-1��1����
��x��-1��-1��y��1ʱ��x=-1��
��-1��x��1��y��1ʱ��y=1��
�ɶԳ��Կɵ���������ͼ�Σ�

�����ۣ��켣����Ϊ��
|x+1|+|y+1|+|x-1|+|y-1|=8��
��x��-1��y��1ʱ��x-y+3=0��
��x��-1��-1��y��1ʱ��x+3=0��
��-1��x��1��y��1ʱ��y=3��
�ɶԳ��Կɵ���������ͼ�Σ�
��3����ͼ�����������ĸ���У�-2��2������-1��2����
��-2��1������-1��1������0��0������1��-1����
��2��-1������1��-2������2��-2����
���ڢ٣���P��x��y�����㵽A��-1��-1����B��1��1������
��ֱ�Ǿ��롱��ȣ�

������|x+1|+|y+1|=|x-1|+|y-1|��
���p��{��x��y��|x+y=0��-1��x��1��x��-1��y��1��x��1��y��-1}����ͼ��
���ڢڣ���P��x��y����C��-2��-2����D��2��2�����㡰ֱ�Ǿ��롱����С��
��D��PA��+D��PB��=|x+2|+|y+2|+|x-2|+|y-2|
=|x+2|+|x-2|+|y+2|+|y-2|
��|x+2+2-x|+|y+2+2-y|=8��
���ҽ���-2��x��2��-2��y��2�Ⱥų�����
�ɵõ�P��{��x��y��|-2��x��2��-2��y��2}����ͼ
��ͬʱ���������٢ڵĸ��������ǣ�
��-2��2������-1��2������-2��1������-1��1������0��0����
��1��-1������2��-1������1��-2������2��-2����
���������⿼���������������켣���̵�������ʱҪ�������⣬ע���������˼��ĺ������ã�

��ϰ��ϵ�д�
 �߽�������ϵ�д�
�߽�������ϵ�д�
�����Ŀ
��֪P����Բ
+
=1�ϵ�һ��������һ�㣬����P��Բx2+y2=16����������PA��PB����A��B���е㣩��ֱ��AB�ֱ�x�ᡢy���ڵ�MN�����MON�����S��MON��O������ԭ�㣩����Сֵ�ǣ�������
| x2 |
| 25 |
| y2 |
| 16 |
A��
| ||
| B��14 | ||
C��
| ||
D��
|
������{an}�ǵȲ����У�������a1=1������d��0��{an}��ǰn���ΪSn���Ҷ�����n��N*���ܴ���m��N*��ʹ��Sn=am����d= ��
������f��x��=
��a��b��R��������ΪR����3a+b��ȡֵ��Χ�ǣ�������
| (a+2)x2+bx+a+2 |
| A��[-2��+�ޣ� |
| B��[-6��+�ޣ� |
| C��[6��+�ޣ� |
| D��[0��+�ޣ� |
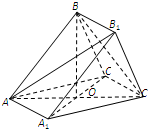 ��ͼ��ʾ��������ABC-A1B1C1�У�AB=AC=AA1=2��ƽ��ABC1��ƽ��A1ACC1��
��ͼ��ʾ��������ABC-A1B1C1�У�AB=AC=AA1=2��ƽ��ABC1��ƽ��A1ACC1��