题目内容
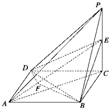
 已知四棱锥P-ABCD的三视图如图所示,E是侧棱PC上的动点.
已知四棱锥P-ABCD的三视图如图所示,E是侧棱PC上的动点.(1)是否无论点E在何位置,都有BD⊥AE?证明你的结论;
(2)求直线PA与底面ABCD所成角的正切值.
考点:直线与平面所成的角,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(1)连结AC,由已知得BD⊥AC,BD⊥PC,从而BD⊥平面PAC,由此得到不论点E在何位置,都有BD⊥AE.
(2)由PC⊥面ABCD,知∠PAC即为直线PA与底面ABCD所成的角,由此能求出直线PA与底面ABCD所成角的正切值.
(2)由PC⊥面ABCD,知∠PAC即为直线PA与底面ABCD所成的角,由此能求出直线PA与底面ABCD所成角的正切值.
解答:
 解:(1)不论点E在何位置,都有BD⊥AE.(1分)
解:(1)不论点E在何位置,都有BD⊥AE.(1分)
证明如下:连结AC,∵ABCD是正方形,∴BD⊥AC.
∵PC⊥底面ABCD,且BD?平面ABCD,∴BD⊥PC.
又∵AC∩PC=C,∴BD⊥平面PAC.
∵不论点E在何位置,都有AE?平面PAC.
∴不论点E在何位置,都有BD⊥AE.(6分)
(2)∵PC⊥面ABCD,
∴∠PAC即为直线PA与底面ABCD所成的角,(8分)
由四棱锥P-ABCD的三视图,知:
AB=1,PC=2,BC=1,
∴AC=
=
,
∴tan∠PAC=
=
=
,
∴直线PA与底面ABCD所成角的正切值为
.(12分)
 解:(1)不论点E在何位置,都有BD⊥AE.(1分)
解:(1)不论点E在何位置,都有BD⊥AE.(1分)证明如下:连结AC,∵ABCD是正方形,∴BD⊥AC.
∵PC⊥底面ABCD,且BD?平面ABCD,∴BD⊥PC.
又∵AC∩PC=C,∴BD⊥平面PAC.
∵不论点E在何位置,都有AE?平面PAC.
∴不论点E在何位置,都有BD⊥AE.(6分)
(2)∵PC⊥面ABCD,
∴∠PAC即为直线PA与底面ABCD所成的角,(8分)
由四棱锥P-ABCD的三视图,知:
AB=1,PC=2,BC=1,
∴AC=
| 1+1 |
| 2 |
∴tan∠PAC=
| PC |
| AC |
| 2 | ||
|
| 2 |
∴直线PA与底面ABCD所成角的正切值为
| 2 |
点评:本题考查直线与平面垂直的证明及应用,考查线面角的正切值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,某公园摩天轮的半径为40m,点O距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处.
如图,某公园摩天轮的半径为40m,点O距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处.