题目内容
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a,b>0)$,过x轴上点P的直线与双曲线的右支交于M,N两点(M在第一象限),直线MO交双曲线左支于点Q(O为坐标原点),连接QN.若∠MPO=60°,∠MNQ=30°,则该双曲线的离心率为$\sqrt{2}$.分析 由题意可得M,Q关于原点对称,即可得到kMN•kQN=$\frac{{b}^{2}}{{a}^{2}}$,分别求出相对应的斜率,再根据离心率公式即可求出
解答  解:由题意可知:M,Q关于原点对称,
解:由题意可知:M,Q关于原点对称,
∴kMN•kQN=$\frac{{b}^{2}}{{a}^{2}}$,
∵kMN=-$\sqrt{3}$,kQN=-$\frac{\sqrt{3}}{3}$,
∴$\frac{{b}^{2}}{{a}^{2}}$=1,
∴e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{2}$
故答案为:$\sqrt{2}$.
点评 本题考查了双曲线的简单性质以及离心率的计算,属于中档题.

练习册系列答案
相关题目
20.(1-2x)3的展开式中所有的二项式系数和为a,函数y=mx-2+1(m>0且m≠1)经过的定点的纵坐标为b,则${({bx+3y})^3}•{({x+\frac{5}{4}y})^5}$的展开式中x6y2的系数为( )
| A. | 320 | B. | 446 | C. | 482 | D. | 248 |
1.如图1为某市2017年2月28天的日空气质量指数折线图.
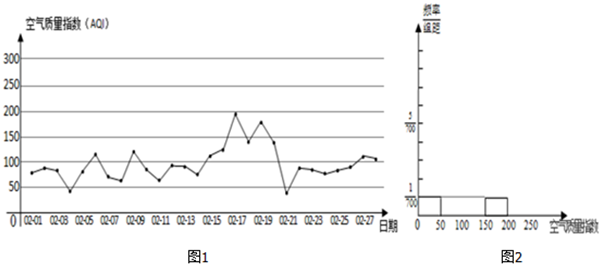
由中国空气质量在线监测分析平台提供的空气质量指数标准如下:
(Ⅰ)请根据所给的折线图补全如图2所示的频率分布直方图(并用铅笔涂黑矩形区域),并估算该市2月份空气质量指数监测数据的平均数(保留小数点后一位);
(Ⅱ)在该月份中任取两天,求空气质量至少有一天为优或良的概率;
(Ⅲ)如果该市对环境进行治理,治理后经统计,每天的空气质量指数近似满足X~N(75,552),则治理后的空气质量指数均值大约下降了多少?

由中国空气质量在线监测分析平台提供的空气质量指数标准如下:
| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | 300以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
(Ⅱ)在该月份中任取两天,求空气质量至少有一天为优或良的概率;
(Ⅲ)如果该市对环境进行治理,治理后经统计,每天的空气质量指数近似满足X~N(75,552),则治理后的空气质量指数均值大约下降了多少?
5.为了研究家用轿车在高速公路上的车速情况,交通部门对100名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在55名男性驾驶员中,平均车速超过100km/h的有45人,不超过100km/h的有10人;在45名女性驾驶员中,平均车速超过100km/h的有25人,不超过100km/h的有20人.
(Ⅰ)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过100km/h与性别有关;
(Ⅱ)在被调查的驾驶员中,按分层抽样的方法从平均车速不超过100km/h的人中抽取6人,再从这6人中采用简单随机抽样的方法随机抽取2人,求这2人恰好为1名男生、1名女生的概率.
参考公式与数据:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
(Ⅰ)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过100km/h与性别有关;
| 平均车速超过100km/h人数 | 平均车速不超过100km/h人数 | 合计 | |
| 男性驾驶人数 | 45 | 10 | 55 |
| 女性驾驶人数 | 25 | 20 | 45 |
| 合计 | 70 | 30 | 100 |
参考公式与数据:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| P(k2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
2.某校高三共有900名学生,高三模拟考之后,为了了解学生学习情况,用分层抽样方法从中抽出若干学生此次数学成绩,按成绩分组,制成如下的频率分布表:
(1)若频数的总和为c,试求a,b,c的值;
(2)为了了解数学成绩在120分以上的学生的心理状态,现决定在第六、七、八组中用分层抽样方法抽取6名学生,在这6名学生中又再随机抽取2名与心理老师面谈,令第七组被抽中的学生数为随机变量ξ,求随机变量ξ的分布列和数学期望;
(3)估计该校本次考试的数学平均分.
| 组号 | 第一组 | 第二组 | 第二组 | 第四组 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 6 | 4 | 22 | 20 |
| 频率 | 0.06 | 0.04 | 0.22 | 0.20 |
| 组号 | 第五组 | 第六组 | 第七组 | 第八组 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 18 | a | 10 | 5 |
| 频率 | b | 0.15 | 0.10 | 0.05 |
(2)为了了解数学成绩在120分以上的学生的心理状态,现决定在第六、七、八组中用分层抽样方法抽取6名学生,在这6名学生中又再随机抽取2名与心理老师面谈,令第七组被抽中的学生数为随机变量ξ,求随机变量ξ的分布列和数学期望;
(3)估计该校本次考试的数学平均分.
19.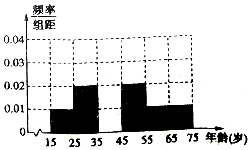 河南多地遭遇年霾,很多学校调整元旦放假时间,提前放假让学生们在家躲霾.郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》,自12月29日12时将黄色预警升级为红色预警,12月30日0时启动Ⅰ级响应,明确要求“幼儿园、中小学等教育机构停课,停课不停学”.学生和家长对停课这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的,某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况整理汇总成如表:
河南多地遭遇年霾,很多学校调整元旦放假时间,提前放假让学生们在家躲霾.郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》,自12月29日12时将黄色预警升级为红色预警,12月30日0时启动Ⅰ级响应,明确要求“幼儿园、中小学等教育机构停课,停课不停学”.学生和家长对停课这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的,某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况整理汇总成如表:
(Ⅰ)请在图中完成被调查人员年龄的频率分布直方图;
(Ⅱ)若从年龄在[25,35),[65,75]两组采访对象中各随机选取2人进行深度跟踪调查,选中4人中不赞成这项举措的人数为X,求随机变量X的分布列和数学期望.
 河南多地遭遇年霾,很多学校调整元旦放假时间,提前放假让学生们在家躲霾.郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》,自12月29日12时将黄色预警升级为红色预警,12月30日0时启动Ⅰ级响应,明确要求“幼儿园、中小学等教育机构停课,停课不停学”.学生和家长对停课这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的,某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况整理汇总成如表:
河南多地遭遇年霾,很多学校调整元旦放假时间,提前放假让学生们在家躲霾.郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》,自12月29日12时将黄色预警升级为红色预警,12月30日0时启动Ⅰ级响应,明确要求“幼儿园、中小学等教育机构停课,停课不停学”.学生和家长对停课这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的,某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况整理汇总成如表:| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(Ⅱ)若从年龄在[25,35),[65,75]两组采访对象中各随机选取2人进行深度跟踪调查,选中4人中不赞成这项举措的人数为X,求随机变量X的分布列和数学期望.