题目内容

1．已知平面向量$\overrightarrow{a}$=（-1，2），$\overrightarrow{b}$=（2，y）且2$\overrightarrow{a}$⊥3$\overrightarrow{b}$，则实数y=1．

分析 求得2$\overrightarrow{a}$=（-2，4），3$\overrightarrow{b}$=（6，3y），再由向量的数量积的坐标表示，计算即可得到y．

解答 解：由2$\overrightarrow{a}$=（-2，4），3$\overrightarrow{b}$=（6，3y），
且2$\overrightarrow{a}$⊥3$\overrightarrow{b}$，
则2$\overrightarrow{a}$•3$\overrightarrow{b}$=0，
即为-2•6+4•3y=0，
即-12+12y=0，
解得y=1．
故答案为：1．

点评 本题考查向量的数量积的坐标表示，考查运算能力，属于基础题．

练习册系列答案
相关题目
11．已知数列{an}的前n项和为Sn，且满足an+2Sn•Sn-1=0（n≥2），a1=$\frac{1}{2}$．
（1）求证：{$\frac{1}{{S}_{n}}$}是等差数列；
（2）求数列{an}的前2011项的和．
12．已知随机变量ξ的分布列如下：
 ξ12345
P0.10.20.40.20.1
则P（2≤ξ＜4）=0.6．
9．在直角坐标系xOy中，已知向量$\overrightarrow{a}$=（-1，2），点A（8，0），B（ksinθ，m）（0≤θ≤$\frac{π}{2}$，m∈R）
（1）若$\overrightarrow{AB}$$⊥\overrightarrow{a}$，且|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|，求向量$\overrightarrow{OB}$的坐标；
（2）若向量$\overrightarrow{AB}$与向量$\overrightarrow{a}$共线，且当k＞4时，msinθ取得最大值4，求$\overrightarrow{OA}•\overrightarrow{OB}$．
16．在△ABC中，CB=4，CA=3，$\overrightarrow{CB}•\overrightarrow{AC}$=-6．
（1）求∠ACB的大小；
（2）若D是AB上一动点，求$\overrightarrow{AD}•$（$\overrightarrow{CA}$+2$\overrightarrow{CB}$）的取值范围．
6．求l：x-2y+1=0被圆C：（x-1）2+y2=1截得的弦长．
13．在△ABC中，AD⊥BC，垂足为D，AD在△ABC的内部，且BD：DC：AD=2：3：6，求∠BAC的度数．
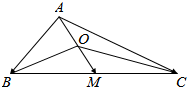10．如图，在△ABC中，O为中线AM上的动点．
（1）证明：$\overrightarrow{OB}$+$\overrightarrow{OC}$=2$\overrightarrow{OM}$
（2）设|$\overrightarrow{AM}$|=2，$\overrightarrow{OM}$=t$\overrightarrow{AM}$（0≤t≤1），试把$\overrightarrow{OA}$•（$\overrightarrow{OB}+\overrightarrow{OC}$）表示为t的函数f（t），并求当O在AM上何处时，f（t）的值最小，最小值是多少？
11．已知函数f（x）的定义域是（0，+∞），f（xy）=f（x）+f（y），且当x＞1时，f（x）＞0．
（1）求f（1）的值；
（2）证明：f（x）在定义域上是增函数；
（3）解不等式f（x（x+$\frac{1}{2}$））≤0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网