题目内容
2．若（$\sqrt{x}$+$\frac{a}{\sqrt{x}}$）4展开式的常数项和为54，且a＞0，则a=3．分析 首先写出二项展开式的通项，整理后得到为常数项时的项，得到关于a的等式．
解答 解；（$\sqrt{x}$+$\frac{a}{\sqrt{x}}$）4展开式的通项为${T}_{r+1}={C}_{4}^{r}（\sqrt{x}）^{4-r}（\frac{a}{\sqrt{x}}）^{r}$=${a}^{r}{C}_{4}^{r}{x}^{2-r}$，r=2时为常数项${a}^{2}{C}_{4}^{2}$=54，a＞0，解得a=3；
故答案为：3．
点评 本题考查二项式定理中特征项的求法问题；属于基础题．
练习册系列答案
相关题目
12．
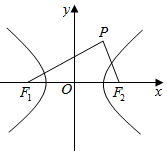如图，已知F1、F2为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，点P在第一象限，且满足（$\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{1}{F}_{2}}$）•$\overrightarrow{{F}_{2}P}$=0，|$\overrightarrow{{F}_{2}P}$|=a，线段PF2与双曲线C交于点Q，若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$，则双曲线C的渐近线方程为（ ）
如图，已知F1、F2为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，点P在第一象限，且满足（$\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{1}{F}_{2}}$）•$\overrightarrow{{F}_{2}P}$=0，|$\overrightarrow{{F}_{2}P}$|=a，线段PF2与双曲线C交于点Q，若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$，则双曲线C的渐近线方程为（ ）| A． | y=±$\frac{1}{2}$x | B． | y=±$\frac{\sqrt{5}}{5}$x | C． | y=±$\frac{2\sqrt{5}}{5}$x | D． | y=±$\frac{\sqrt{3}}{3}$x |
14．假设你家订了一份牛奶，送奶工人在早上6：00-7：00之间把牛奶送到你家，你离开家去上学的时间在早上6：30-7：30之间，则你在离开家前能收到牛奶的概率是（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{5}{8}$ | C． | $\frac{1}{2}$ | D． | $\frac{7}{8}$ |
11．若a=（$\frac{1}{2}$）${\;}^{\frac{1}{3}}$，b=$lo{g_{\frac{1}{3}}}$2，c=lo${g_{\frac{1}{2}}}$3，则a，b，c三者的大小关系是（ ）
| A． | b＞c＞a | B． | c＞a＞b | C． | a＞b＞c | D． | a＞c＞b |
12．已知全集U=R，集合P={x|x2-2x≤0}，Q={y|y=x2-2x}，则P∩Q为（ ）
| A． | [-1，2] | B． | [0，2] | C． | [0，+∞） | D． | [-1，+∞） |