题目内容
下列几个命题:
①“
”是“一元二次不等式ax2+bx+c≥0的解集为R”的充要条件;
②设函数y=f(x)定义域为R,则函数y=f(x)与y=f(-x)的图象关于y轴对称;
③若函数y=Acos(ωx+φ)(A≠0)为奇函数,则φ=
+kπ(k∈Z);
④已知x∈(0,π),则y=sinx+
的最小值为2
.
其中正确的有( )
①“
|
②设函数y=f(x)定义域为R,则函数y=f(x)与y=f(-x)的图象关于y轴对称;
③若函数y=Acos(ωx+φ)(A≠0)为奇函数,则φ=
| π |
| 2 |
④已知x∈(0,π),则y=sinx+
| 2 |
| sinx |
| 2 |
其中正确的有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:①由一元二次不等式ax2+bx+c≥0的解集为R?
,可判断①的正误;
②利用函数的对称轴可判断②的正误;
③利用正弦函数与余弦函数的奇偶性质可判断③的正误;
④x∈(0,π)⇒0<sinx≤1,令t=sinx(0<t≤1),g(t)=t+
(0<t≤1),利用双钩函数的单调性与最值可求得g(t)min=g(1)=3,可判断④的正误.
|
②利用函数的对称轴可判断②的正误;
③利用正弦函数与余弦函数的奇偶性质可判断③的正误;
④x∈(0,π)⇒0<sinx≤1,令t=sinx(0<t≤1),g(t)=t+
| 2 |
| t |
解答:
解:①
⇒一元二次不等式ax2+bx+c≥0的解集为R,即充分性成立;
反之,一元二次不等式ax2+bx+c≥0的解集为R,则
,即必要性成立;
所以“
”是“一元二次不等式ax2+bx+c≥0的解集为R”的充要条件,即①正确;
②设函数y=f(x)定义域为R,则函数y=f(x)与y=f(-x)的图象关于y轴对称,正确;
③若函数y=Acos(ωx+φ)(A≠0)为奇函数,则φ=
+kπ(k∈Z),正确;
④∵x∈(0,π),
∴0<sinx≤1,令t=sinx(0<t≤1),g(t)=t+
(0<t≤1),当0<t≤1时,g′(t)=1-
<0,
双钩函数g(t)=t+
在(0,
]单调递减,
∴g(t)min=g(1)=3,
∴y=sinx+
的最小值为3,故④错误.
故选:D.
|
反之,一元二次不等式ax2+bx+c≥0的解集为R,则
|
所以“
|
②设函数y=f(x)定义域为R,则函数y=f(x)与y=f(-x)的图象关于y轴对称,正确;
③若函数y=Acos(ωx+φ)(A≠0)为奇函数,则φ=
| π |
| 2 |
④∵x∈(0,π),
∴0<sinx≤1,令t=sinx(0<t≤1),g(t)=t+
| 2 |
| t |
| 2 |
| t2 |
双钩函数g(t)=t+
| 2 |
| t |
| 2 |
∴g(t)min=g(1)=3,
∴y=sinx+
| 2 |
| sinx |
故选:D.
点评:本题考查命题的真假判断与应用,着重考查函数的对称性、单调性及最值及恒成立问题,考查充分必要条件的概念,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设集合A={2,3,5,8},B={3,5,7,9},则集合A∩B=( )
| A、{2,3,5,7,8} |
| B、{5} |
| C、{3,5} |
| D、{2,8,7,9} |
如图程序运行后输出的结果为( )


| A、22;-22 |
| B、-22;22 |
| C、6;-6 |
| D、-6;6 |
若变量x,y满足条件
,则z=x+y的取值范围是( )
|
| A、(-∞,3] |
| B、[3,+∞) |
| C、[0,3] |
| D、[1,3] |
已知函数y=f(x)是定义在(-1,1)上的函数,且对于任意x1,x2∈(-1,1)且x1≠x2,都有
<0,则关于a的不等式f(1-a)<f(a2-1)的取值范围是( )
| f(x1)-f(x2) |
| x 1-x2 |
| A、-2<a<1 | ||
| B、a>1或a<-2 | ||
C、0<a<
| ||
| D、0<a<1 |
函数f(x)=x2+alnx在x=1处取得极值,则a等于( )
| A、2 | B、-2 | C、4 | D、-4 |
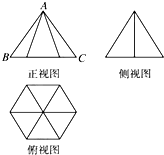 一个几何体的三视图如图所示,其中正视图中△ABC是边长为2的正三角形,俯视图为正六边形,求该几何体的侧视图的面积.
一个几何体的三视图如图所示,其中正视图中△ABC是边长为2的正三角形,俯视图为正六边形,求该几何体的侧视图的面积.