题目内容
【题目】已知函数
．
（1）若方程
有两个小于2的不等实根，求实数a的取值范围；
（2）若不等式
对任意
恒成立，求实数a的取值范围；
（3）若函数
在[0，2]上的最大值为4，求实数a的值．
【答案】（1）
（2）
（3）
或
【解析】试题分析：（1）根据二次函数的图象与性质得到关于
的不等式组，解出即可；（2）问题转化为
的任意
，根据
，求出的取值范围即可；（3）求出函数的对称轴，通过讨论的范围结合二次函数的性质，求出的范围即可.
试题解析：（1）方程
有两个小于2的不等实根
;
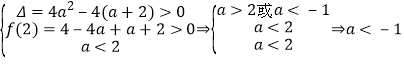（2）由
得
对任意恒成立，则
;
（3）函数
的对称轴为x=a，则
当a<1时，函数在[0，2]上的最大值为
，符合条件；
当a≥1时，函数在[0，2]上的最大值为
，符合条件；
所以，所求实数a的值为或．
【方法点晴】本题主要考查不等式恒成立问题，属于难题．不等式恒成立问题常见方法：① 分离参数
恒成立(
可)或
恒成立（
即可）；② 数形结合(
图象在
上方即可)；③ 讨论最值
或
恒成立；④一元二次不等式任意恒成立可用判别式小于零解答.本题（2）是利用方法④ 求得的取值范围.
练习册系列答案
相关题目
【题目】我国的高铁技术发展迅速，铁道部门计划在
两城市之间开通高速列车，假设列车在试运行期间，每天在
两个时间段内各发一趟由
城开往
城的列车（两车发车情况互不影响），
城发车时间及概率如下表所示：
发车 时间 |
|
|
|
|
|
|
概率 |
|
|
|
|
|
|
若甲、乙两位旅客打算从城到
城，他们到达
火车站的时间分别是周六的
和周日的
（只考虑候车时间，不考虑其他因素）．
（1）设乙候车所需时间为随机变量
（单位：分钟），求
的分布列和数学期望
；
（2）求甲、乙两人候车时间相等的概率．
