题目内容
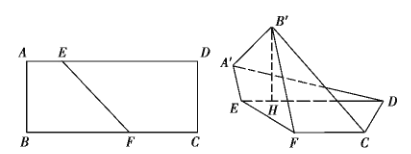
【题目】已知矩形
中，
，
分别在
上，且
，沿
将四边形
折成四边形
，使点
在平面
上的射影
在直线
上，且
.
（1）求证：
平面
；
（2）求
到平面
的距离.
【答案】（1）详见解析（2）
【解析】
试题分析：（1）证明线面平行，一般利用线面平行判定定理，即从线线平行出发给予证明，而当线线平行比较难找时，可以先证面面平行，再转化为线面平行：本题有两组相交直线互相平行，
及
，先得线面平行，
平面
及
平面，再得面面平行，平面
平面
，最后得线面平行
平面（2）求点到直线距离，一般利用等体积法，即利用高求对应点到面的距离：因为
，所以
试题解析：（1）证明：∵
，∴，又
平面
，
平面
∴平面
同理又，平面
且
，∴平面平面
又
平面，∴平面
（2）由题可知，
，
，∵
底面
，∴
又
，∴
，
，
，∴
∴.
练习册系列答案
相关题目
