题目内容
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]()
![]() 为平面上的动点,且过点
为平面上的动点,且过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,满足:
,满足:![]()
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)在轨迹![]() 上求一点
上求一点![]() ,使得
,使得![]() 到直线
到直线![]() 的距离最短,并求出最短距离.
的距离最短,并求出最短距离.
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
【解析】
试题分析:(Ⅰ)将点的坐标代入![]() 化简可得到动点
化简可得到动点![]() 的轨迹
的轨迹![]() 的方程;(Ⅱ)由点到直线的距离公式求得M到直线的距离,结合函数性质可求得函数的最小值及取得最小值时的自变量值即M的坐标
的方程;(Ⅱ)由点到直线的距离公式求得M到直线的距离,结合函数性质可求得函数的最小值及取得最小值时的自变量值即M的坐标
试题解析:(Ⅰ)设![]() ,
,
![]() ,…………4分,
,…………4分,
![]() ,
,![]() ,
,
所求轨迹为:![]() ………6分
………6分
(Ⅱ)法一:设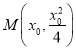 ,则
,则![]() 的距离为
的距离为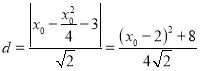
![]() ,此时
,此时![]() 为所求. ……12分
为所求. ……12分
法二:当与直线![]() 平行,且与曲线相切时的切点与与直线
平行,且与曲线相切时的切点与与直线![]() 的距离最短.
的距离最短.
设该直线方程为![]() ,…… 7分
,…… 7分
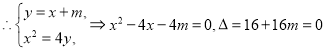 ,解得:
,解得:![]()
![]() 到直线
到直线![]() 的距离最短,最短距离为
的距离最短,最短距离为![]() .……12分
.……12分
法三:当与直线![]() 平行,且与曲线相切时的切点与与直线
平行,且与曲线相切时的切点与与直线![]() 的距离最短.
的距离最短.
设切点为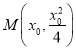 ,轨迹方程可化为:
,轨迹方程可化为:![]() ,切线斜率为
,切线斜率为![]() ,
,
以下方法同法二.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目