Question

设平面α∥平面β，A、C∈α，B、D∈β，直线AB与CD交于点S，且AS=8，BS=9，CD=34，①当S在α、β之间时，SC=

 

，②当S不在α、β之间时，SC=

 

．

Answer 1

分析：因为平面α∥平面β，且A、C∈α，B、D∈β，直线AB与CD交于点S，所以根据平面与平面平行的性质定理可得：两条交线应该平行，连接AC、BD，即AC∥BD，所以△SAC∽△SBD，又根据相似比的概念及AS=8，BS=9，CD=34，则：①SC=16，②SC=272．

解答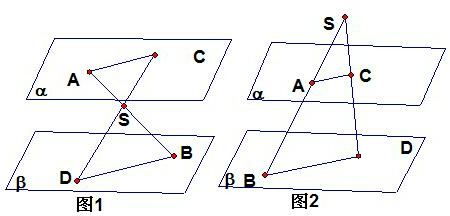：解：
∵平面α∥平面β，A、C∈α，B、D∈β，直线AB与CD交于点S，
∴根据平面与平面平行的性质定理可得：AC∥BD，
∴△SAC∽△SBD，
①∴

SC

SD

=

AS

SB

=

8

9

，且SC+SD=CD=34，则：SC=16；
②∴

SC

SD

=

AS

SB

=

8

9

，且SD-SC=CD=34，则：SC=272．
故答案为：①SC=16，②SC=272．

点评：本题主要考查了空间中直线与平面平行的性质，相似三角形的判定，考查空间想象能力和思维能力．