题目内容
已知p≠0,数列{an}满足:a1=2,an+1=pan+1-p(n∈N*)
(1)求数列{an}的通项公式;
(2)bn=2-qn-1(n∈N*),当n≥2时,p,q都在区间(0,1)内变化,且满足p2n-2+q2n-2≤1时,求所有点(an,bn)所构成图形的面积;
(3)当p>1时,证明:
<
+
+…+
<
(n∈N*)
(1)求数列{an}的通项公式;
(2)bn=2-qn-1(n∈N*),当n≥2时,p,q都在区间(0,1)内变化,且满足p2n-2+q2n-2≤1时,求所有点(an,bn)所构成图形的面积;
(3)当p>1时,证明:
| n |
| p |
| a1 |
| a2 |
| a2 |
| a3 |
| an |
| an+1 |
| n+1 |
| p |
考点:数列与不等式的综合,数列递推式
专题:综合题,等差数列与等比数列
分析:(1)先证明{an-1}是以2为首项,p为公比的等比数列,即可求数列{an}的通项公式;
(2)确定对满足题设的所有点(an,bn)在区域Ω:
内,即可求所有点(an,bn)所构成图形的面积;
(3)利用放缩法进行证明即可.
(2)确定对满足题设的所有点(an,bn)在区域Ω:
|
(3)利用放缩法进行证明即可.
解答:
 (1)解:∵an+1=pan+1-p(n∈N*)
(1)解:∵an+1=pan+1-p(n∈N*)
∴an+1-1=p(an-1)(n∈N*) …(2分)
∴{an-1}是以2为首项,p为公比的等比数列
因此an-1=pn-1,即an=1+pn-1 …(4分)
(2)解:∵当n≥2时,an=1+pn-1,bn=2-qn-1,
由p,q都在区间(0,1)内变化,得1<an<2,1<bn<2 …(6分)
∵p2n-2+q2n-2≤1,
∴(an-1)2+(bn+1)2≤1
即对满足题设的所有点(an,bn)在区域Ω:
内…(8分)
而对区域Ω内的任一点(x,y),
取p=
,q=
,
则an=1+pn-1,bn=2-qn-1,即?p,q∈(0,1),使得?(x,y)∈Ω,(x,y)都是(an,bn)中的点
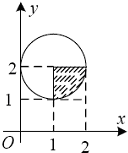
综上可知,点(an,bn)构成的图形是如图所示的
圆,其面积为
…(10分)
(3)证明:∵
=
>
∴
+
+…+
>
…(12分)
∵
=
<
+
•
…(14分)
∴
+
+…+
<
+
(
+
+…
)<
∴
<
+
+…+
<
…(16分)
 (1)解:∵an+1=pan+1-p(n∈N*)
(1)解:∵an+1=pan+1-p(n∈N*)∴an+1-1=p(an-1)(n∈N*) …(2分)
∴{an-1}是以2为首项,p为公比的等比数列
因此an-1=pn-1,即an=1+pn-1 …(4分)
(2)解:∵当n≥2时,an=1+pn-1,bn=2-qn-1,
由p,q都在区间(0,1)内变化,得1<an<2,1<bn<2 …(6分)
∵p2n-2+q2n-2≤1,
∴(an-1)2+(bn+1)2≤1
即对满足题设的所有点(an,bn)在区域Ω:
|
而对区域Ω内的任一点(x,y),
取p=
| n-1 | x-1 |
| n-1 | 2-y |
则an=1+pn-1,bn=2-qn-1,即?p,q∈(0,1),使得?(x,y)∈Ω,(x,y)都是(an,bn)中的点
综上可知,点(an,bn)构成的图形是如图所示的
| 1 |
| 4 |
| π |
| 4 |
(3)证明:∵
| ak |
| ak+1 |
| 1+pk-1 |
| 1+pk |
| 1 |
| p |
∴
| a1 |
| a2 |
| a2 |
| a3 |
| an |
| an+1 |
| n |
| p |
∵
| ak |
| ak+1 |
| 1+pk-1 |
| 1+pk |
| 1 |
| p |
| p-1 |
| p |
| 1 |
| pk |
∴
| a1 |
| a2 |
| a2 |
| a3 |
| an |
| an+1 |
| n |
| p |
| p-1 |
| p |
| 1 |
| p |
| 1 |
| p2 |
| 1 |
| pn |
| n+1 |
| p |
∴
| n |
| p |
| a1 |
| a2 |
| a2 |
| a3 |
| an |
| an+1 |
| n+1 |
| p |
点评:本题考查等比数列的证明,考查数列的通项,考查不等式的证明,考查学生分析解决问题的能力,有难度.

练习册系列答案
相关题目

 已知三棱柱ABC-A1B1C1中,平面A1AC⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2.
已知三棱柱ABC-A1B1C1中,平面A1AC⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2.