题目内容
如图,三棱锥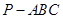 中,
中,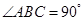 ,
,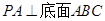

(Ⅰ)求证: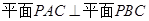 ;
;
(Ⅱ)若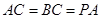 ,
,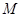 是
是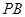 的中点,求
的中点,求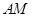 与平面
与平面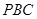 所成角的正切值
所成角的正切值
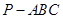 中,
中,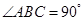 ,
,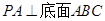

(Ⅰ)求证:
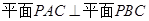 ;
;(Ⅱ)若
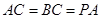 ,
,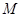 是
是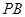 的中点,求
的中点,求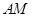 与平面
与平面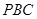 所成角的正切值
所成角的正切值 (Ⅰ)证明略;(Ⅱ)

试题分析:(Ⅰ)根据直线与平面垂直的判定定理,只要找到
 和平面
和平面 中两条相交直线垂直就可以证明直线和平面垂直,那么再由平面和平面垂直的判定定理可知
中两条相交直线垂直就可以证明直线和平面垂直,那么再由平面和平面垂直的判定定理可知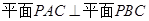 ,证明中要把条件到结论叙述清楚;(Ⅱ)先根据
,证明中要把条件到结论叙述清楚;(Ⅱ)先根据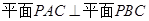 这个条件做辅助线构造出所求的线面角,再在三角形中根据解三角形的方法求得线面角的正切值,一定要注意线面角要找准,不能乱构造
这个条件做辅助线构造出所求的线面角,再在三角形中根据解三角形的方法求得线面角的正切值,一定要注意线面角要找准,不能乱构造 试题解析:解:(Ⅰ)因为
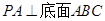 ,所以
,所以 2分
2分又因为
 ,即
,即
所以
 4分
4分又
 ,所以
,所以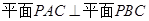 6分
6分(Ⅱ)取
 中点
中点 ,连
,连 ,则
,则

又
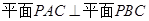 ,所以
,所以 ,连结
,连结 ,
,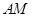 ,
,则
 就是
就是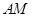 与平面
与平面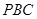 所成的角 10分
所成的角 10分设
 ,则
,则 ,
, ,
,所以
 15分
15分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
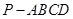 中,底面
中,底面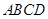 为菱形,
为菱形,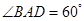 ,
,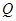 为
为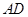 的中点.
的中点.
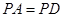 ,求证:平面
,求证:平面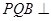 平面
平面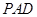 ;
; 在线段
在线段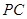 上,
上,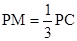 ,若平面
,若平面 平面
平面 ,且
,且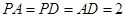 ,求二面角
,求二面角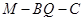 的大小.
的大小.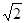 , BD=BC=1, AA1=2,E为DC的中点,F是棱DD1上的动点.
, BD=BC=1, AA1=2,E为DC的中点,F是棱DD1上的动点.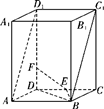
 中,AD∥BC,
中,AD∥BC, 平面
平面 ,
,  ,BC=6.
,BC=6.
 的余弦值.
的余弦值.
 ,求证:平面ADE⊥平面PBC
,求证:平面ADE⊥平面PBC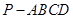 中,底面
中,底面 为直角梯形,
为直角梯形,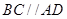 、
、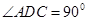 ,
,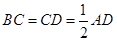 ,
,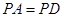 ,
,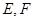 为
为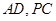 的中点.
的中点.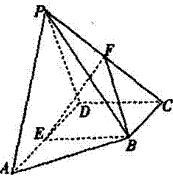
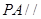 平面
平面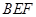 ;
;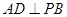 .
.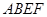 所在平面与直角梯形
所在平面与直角梯形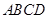 所在平面互相垂直,
所在平面互相垂直,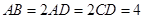 ,
,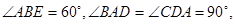 点
点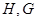 分别是线段
分别是线段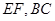 的中点.
的中点. 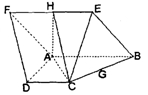
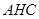
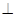 平面
平面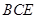 ;
;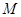 在直线
在直线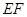 上,且
上,且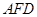 ,求平面
,求平面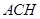 与平面
与平面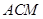 所成角的余弦值。
所成角的余弦值。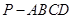 的底面是正方形,
的底面是正方形,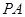 ⊥底面
⊥底面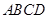 ,且
,且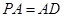 ,点
,点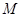 、
、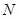 分别为侧棱
分别为侧棱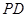 、
、 的中点
的中点 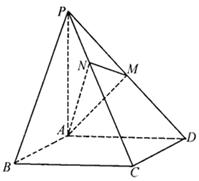
 ∥平面
∥平面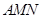 ;
;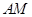 ⊥平面
⊥平面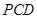 .
.