题目内容
在△ABC中，已知AB=2，BC=3，∠ABC=60°AH⊥BC于H，M为AH的中点，若
=λ
+μ
，则λ+μ的值是（ ）
| AM |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：利用向量的运算法则即可得出．
解答：
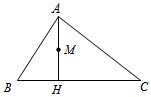解：如图所示，
∵AB=2，BC=3，∠ABC=60°AH⊥BC于H，M为AH的中点
∴BH=1，
∴
=
∴
=
=
（
+
）=
+
=
+
（
-
）=
+
，
∵
=λ
+μ
，
∴λ=
，μ=
，
∴λ+μ=
故选：D．
解：如图所示，∵AB=2，BC=3，∠ABC=60°AH⊥BC于H，M为AH的中点
∴BH=1，
∴
| BH |
| 1 |
| 3 |
| BC |
∴
| AM |
| 1 |
| 2 |
| AH |
| 1 |
| 2 |
| AB |
| BH |
| 1 |
| 2 |
| AB |
| 1 |
| 6 |
| BC |
| 1 |
| 2 |
| AB |
| 1 |
| 6 |
| AC |
| AB |
| 1 |
| 3 |
| AB |
| 1 |
| 6 |
| AC |
∵
| AM |
| AB |
| AC |
∴λ=
| 1 |
| 3 |
| 1 |
| 6 |
∴λ+μ=
| 1 |
| 2 |
故选：D．
点评：本题主要考查了向量的几何意义，熟练掌握向量的运算法则是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
若a+b=0，则直线y=ax+b的图象可能是（ ）
A、 |
B、 |
C、 |
D、 |
已知映射f：A→B，其中集合A={-9，-3，-1，1，3，9}，集合B中的元素都是A中的元素在映射f下的象，且对于任意x∈A，在B中和它对应的元素是log3|x|，则集合B为（ ）
| A、{1，2，3} |
| B、{0，1，2} |
| C、{-2，-1，0，1，2} |
| D、{1，2} |
如图，平面内的两条相交直线OP1和OP2将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ（不包含边界），设
| OP |
| OP1 |
| OP2 |
| A、m＞0，n＞0 |
| B、m＞0，n＜0 |
| C、m＜0，n＞0 |
| D、m＜0，n＜0 |