题目内容
12.已知命题p:|x+1|>2,命题q:5x-6>x2,则p是q的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 把p和q中的不等式解出,根据解出的x的范围分析p与q的互推情况,从而判断p是q的什么条件.
解答 解:由5x-6≥x2,得2≤x≤3;
由|x+1|>2,得:x<-3或x>1.
由2≤x≤3能推出x<-3或x>1,反之,由x<-3或x>1不能推出2≤x≤3,
所以由q能推出p,由p不能推出q,即p是q的必要不充分条件.
故选:B.
点评 本题考查了必要条件、充分条件与充要条件,判断充要条件的方法是:
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
此题是基础题.

练习册系列答案
相关题目
2.在公差d=3的等差数列{an}中,a2+a4=-2,则数列{|an|}的前10项和为( )
| A. | 127 | B. | 125 | C. | 89 | D. | 70 |
3.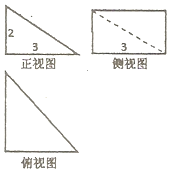 已知一几何体的正视图、俯视图为直角三角形,侧视图为矩形,则该几何体的体积为( )
已知一几何体的正视图、俯视图为直角三角形,侧视图为矩形,则该几何体的体积为( )
 已知一几何体的正视图、俯视图为直角三角形,侧视图为矩形,则该几何体的体积为( )
已知一几何体的正视图、俯视图为直角三角形,侧视图为矩形,则该几何体的体积为( )| A. | 6 | B. | 12 | C. | 18 | D. | 36 |
20.双曲线的渐近线方程为y=±4x,则该双曲线的离心率为( )
| A. | 5 | B. | $\sqrt{5}$ | C. | $\sqrt{17}$或$\frac{\sqrt{17}}{4}$ | D. | $\sqrt{17}$或$\frac{\sqrt{17}}{2}$ |