题目内容
19.已知△ABC的三个内角A,B,C所对的边分别为a,b,c,且b2+c2=a2+bc(1)求A;
(2)若$a=\sqrt{3}$,b+c=3,求△ABC的面积.
分析 (1)由题意可得b2+c2-a2=bc,整体代入余弦定理可得cosA,由三角形内角的范围可得A=$\frac{π}{3}$;
(2)由题意和余弦定理可得bc=2,整体代入三角形的面积公式计算可得.
解答 解:(1)∵△ABC中,b2+c2=a2+bc,
∴b2+c2-a2=bc,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{2}$,
又∵A∈(0,π),∴A=$\frac{π}{3}$;
(2)∵$a=\sqrt{3}$,b+c=3,A=$\frac{π}{3}$,
由余弦定理可得a2=b2+c2-2bccosA
=b2+c2-bc=(b+c)2-3bc,
代入数据可得3=9-3bc,解得bc=2,
∴△ABC的面积S=$\frac{1}{2}$bcsinA=$\frac{1}{2}$×2×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查正余弦定理解三角形,涉及三角形的面积公式和整体代入的思想,属中档题.

练习册系列答案
相关题目
7.当a为任意实数时,直线(a-1)x-y-a-1=0恒过定点C,则以C为圆心,半径为$\sqrt{5}$的圆的方程为( )
| A. | x2+y2-2x+4y=0 | B. | x2+y2+2x+4y=0 | C. | x2+y2+2x-4y=0 | D. | x2+y2-2x-4y=0 |
14.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}+1,x<1}\\{{x}^{2}+mx,x≥1}\end{array}\right.$,若f(f(0))=6m,则实数m等于( )
| A. | $\frac{1}{5}$ | B. | $\frac{4}{5}$ | C. | 1 | D. | 6 |
4.下列函数中,既是偶函数又在(0,+∞)单调递增的函数是( )
| A. | y=x3 | B. | y=|x|+1 | C. | y=-x2+1 | D. | y=2x |
9.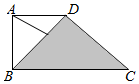 如图,在直角梯形ABCD中,DA=AB=1,BC=2,点P在阴影区域(含边界)中运动,则有$\overrightarrow{AP}•\overrightarrow{BD}$的取值范围是( )
如图,在直角梯形ABCD中,DA=AB=1,BC=2,点P在阴影区域(含边界)中运动,则有$\overrightarrow{AP}•\overrightarrow{BD}$的取值范围是( )
 如图,在直角梯形ABCD中,DA=AB=1,BC=2,点P在阴影区域(含边界)中运动,则有$\overrightarrow{AP}•\overrightarrow{BD}$的取值范围是( )
如图,在直角梯形ABCD中,DA=AB=1,BC=2,点P在阴影区域(含边界)中运动,则有$\overrightarrow{AP}•\overrightarrow{BD}$的取值范围是( )| A. | [-1,1] | B. | $[{-1,\frac{1}{2}}]$ | C. | $[{-\frac{1}{2},1}]$ | D. | [-1,0] |