题目内容
已知 为
为 的内角
的内角 的对边,满足
的对边,满足 ,函数
,函数
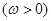 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减.
上单调递减.
(Ⅰ)证明: ;
;
(Ⅱ)若 ,证明
,证明 为等边三角形.
为等边三角形.
(1)根据正弦定理和两角和差关系的运用来得到证明。
(2)根据余弦定理得到三边长度相等来得到结论。
解析试题分析:解:(Ⅰ)根据题意,由于 ,根据正弦定理,可知
,根据正弦定理,可知 ,
,
故可知
(Ⅱ)由题意知:由题意知: ,解得:
,解得: , 8分
, 8分
因为 ,
,  ,所以
,所以 9分
9分
由余弦定理知: 10分
10分
所以 因为
因为 ,所以
,所以 ,
,
即: 所以
所以 11分
11分
又 ,所以
,所以 为等边三角形. 12分
为等边三角形. 12分
考点:解三角形
点评:主要是考查了解三角形的运用,属于基础题。

练习册系列答案
相关题目
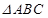 中,角
中,角 所对的边为
所对的边为 ,角
,角 为锐角,若
为锐角,若 ,
, 且
且 .
. 的大小;
的大小; ,求
,求 .
. 、圆心角为60°的扇形的
、圆心角为60°的扇形的 弧上任取一点
弧上任取一点 ,作扇形的内接矩形
,作扇形的内接矩形 ,使点
,使点 在
在 上,点
上,点 在
在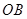 上,设矩形
上,设矩形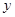 .
.
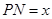 ,将
,将 的函数关系式;
的函数关系式;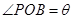 ,将
,将 的函数关系式.
的函数关系式.
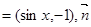
 ,
,
 时,求函数
时,求函数 的值域:
的值域: 中,
中, 分别为角
分别为角 的对边,若
的对边,若 ,求边
,求边 .
. 且
且 ,求:
,求: 的值.
的值. ------①
------① ------②
------② ------③
------③ 有
有
 .
. ;
; 的三个内角
的三个内角 满足
满足 ,试判断
,试判断 <α<
<α< ,0<β<
,0<β< ,
, +β)=
+β)= ,求sin(α+β)的值.
,求sin(α+β)的值. 中,以
中,以 轴为始边做两个锐角
轴为始边做两个锐角 ,
, ,它们的终边分别与单位圆相交于
,它们的终边分别与单位圆相交于 两点,已知点
两点,已知点 的横坐标为
的横坐标为 ,点
,点 的纵坐标为
的纵坐标为 .
. 的值;
的值; 的值.
的值. 为锐角,
为锐角, ,
, ,求
,求 和
和 的值。
的值。