题目内容
8.计算$cos({π+\frac{π}{3}})cos({2π+\frac{π}{3}})cos({3π+\frac{π}{3}})…cos({100π+\frac{π}{3}})$得( )| A. | $\frac{1}{{{2^{100}}}}$ | B. | $-\frac{1}{{{2^{100}}}}$ | C. | $\frac{1}{{{2^{50}}}}$ | D. | $-\frac{1}{{{2^{50}}}}$ |
分析 利用诱导公式化简所求,进而计算得解.
解答 解:$cos({π+\frac{π}{3}})cos({2π+\frac{π}{3}})cos({3π+\frac{π}{3}})…cos({100π+\frac{π}{3}})$
=[(-$\frac{1}{2}$)×$\frac{1}{2}$]50
=$\frac{1}{{2}^{100}}$.
故选:A.
点评 本题主要考查了诱导公式在三角函数化简求值中的应用,考查了计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 8 | B. | $6\sqrt{2}$ | C. | $4\sqrt{2}$ | D. | 4 |
20.若f(x)=ex-ax2+(a-e)x有三个不同的零点,则实数a的取值范围是( )
| A. | (0,+∞) | B. | (0,e) | C. | [1,e) | D. | (e,+∞) |
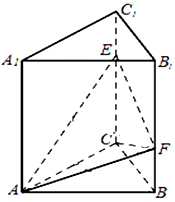 如图,三棱柱ABC-A1B1C1的底面是边长为2的等边三角形,AA1⊥底面ABC,点E,F分别是棱CC1,BB1上的点,且EC=B1F=2FB.
如图,三棱柱ABC-A1B1C1的底面是边长为2的等边三角形,AA1⊥底面ABC,点E,F分别是棱CC1,BB1上的点,且EC=B1F=2FB.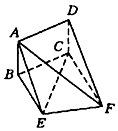 如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,∠BCF=∠CEF=90°.AD=$\sqrt{3}$,EF=2
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,∠BCF=∠CEF=90°.AD=$\sqrt{3}$,EF=2