题目内容
20. 已知函数$g(x)=2sin(2ωx+\frac{π}{6})$(其中0<ω<1),若点$(-\frac{π}{6},0)$是函数g(x)图象的一个对称中心,
已知函数$g(x)=2sin(2ωx+\frac{π}{6})$(其中0<ω<1),若点$(-\frac{π}{6},0)$是函数g(x)图象的一个对称中心,(1)试求ω的值;
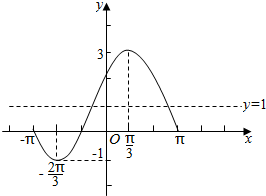
(2)若f(x)=g(x)+1,请先列表再作出函数f(x)在区间x∈[-π,π]上的图象.
分析 (1)根据三角函数的对称性即可求出ω的值.
(2)用五点法作出函数在区间[-π,π]上的图象.
解答 解:(1)∵点$(-\frac{π}{6},0)$是函数g(x)图象的一个对称中心,
∴$-\frac{π}{6}$×2ω+$\frac{π}{6}$=kπ,
即ω=$\frac{1}{2}$-3k,
∵0<ω<1,∴当k=0时,ω=$\frac{1}{2}$.
(2)∵ω=$\frac{1}{2}$,则g(x)=2sin(x+$\frac{π}{6}$),
∴f(x)=g(x)+1=2sin(x+$\frac{π}{6}$)+1,
列表
| x+$\frac{π}{6}$ | -$\frac{5π}{6}$ | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | π | $\frac{7π}{6}$ |
| x | -π | -$\frac{2π}{3}$ | -$\frac{π}{6}$ | $\frac{π}{3}$ | $\frac{5π}{6}$ | π |
| f(x) | 0 | -1 | 1 | 3 | 1 | 0 |
点评 本题主要考查三角函数对称性的应用,已经三角函数函数图象的作法,要求熟练掌握用五点法作出函数y=Asin(ωx+φ)在一个周期上的简图,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.动点A在圆x2+y2=1上移动时,它与定点B(3,0)连线的中点的轨迹方程是( )
| A. | x2+y2+3x+2=0 | B. | x2+y2-3x+2=0 | C. | x2+y2+3y+2=0 | D. | x2+y2-3y+2=0 |
15.某工人生产合格零售的产量逐月增长,前5个月的产量如表所示:请根据所级5组数据,求出y关于x的线性回归方程$\hat y$=x+4.
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 合格零件y(件) | 5 | 6 | 7 | 8 | 9 |
12.命题p:?a∈(-∞,-$\frac{1}{4}$),使得函数f(x)=|x+$\frac{a}{x+1}$|在[$\frac{1}{2}$,3]上单调递增,命题q:g(x)=x+log2x在区间($\frac{1}{2}$,+∞)上无零点,则下列命题中正确的是( )
| A. | ¬p | B. | p∧q | C. | (¬p)∨q | D. | p∧(¬q) |
10.样本数据:-2,-1,0,1,2的方差为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 1 | D. | 2.5 |