题目内容
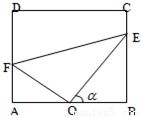
 某小区规划一块周长为2a(a为正常数)的矩形停车场,其中如图所示的直角三角形ADP内为绿化区域.且∠PAC=∠CAB.设矩形的长AB=x,AB>AD
某小区规划一块周长为2a(a为正常数)的矩形停车场,其中如图所示的直角三角形ADP内为绿化区域.且∠PAC=∠CAB.设矩形的长AB=x,AB>AD(1)求线段DP的长关于x的函数l(x)表达式并指出定义域;
(2)应如何规划矩形的长AB,使得绿化面积最大?
分析:(1)由已知中矩形停车场的周长为2a(a为正常数),直角三角形ADP内为绿化区域.且∠PAC=∠CAB.我们易得tan2α=tan∠APD=
,进而根据矩形的长AB=x,AB>AD,可求出线段DP的长关于x的函数l(x)表达式并指出定义域;
(2)由(1)中函数的解析式,我们易求出绿化区域即直角三角形ADP面积的表达式,进而利用基本不等式,我们可求出直角三角形ADP面积取最大值时,对应的AB的长,即可得到答案.
| AD |
| DP |
(2)由(1)中函数的解析式,我们易求出绿化区域即直角三角形ADP面积的表达式,进而利用基本不等式,我们可求出直角三角形ADP面积取最大值时,对应的AB的长,即可得到答案.
解答:解:(1)AD=BC=a-x,由AB>AD,得
<x<a(a>0)
设∠BAC=∠CAP=α,tanα=
,因为∠APD=2α,tan2α=
=
,
得DP=
,
所以 l(x)=
,定义域为(
,a)-----------------------------(7分)
(2)S△ADP=
AD•DP=
(3a-
-2x)---------------------------------(9分)
因为
+2x≥2a
,仅当x=
a时取等号.又
a∈(
,a)
所以(S△ADP)max=
(3-2
),此时AB=
a-------------------------------(13分)
答:当矩形的长为
a时,绿化面积最大.----------------------------------------(14分)
| a |
| 2 |
设∠BAC=∠CAP=α,tanα=
| a-x |
| x |
| AD |
| DP |
| a-x |
| DP |
得DP=
| 2ax-a2 |
| 2x |
所以 l(x)=
| 2ax-a2 |
| 2x |
| a |
| 2 |
(2)S△ADP=
| 1 |
| 2 |
| a |
| 4 |
| a2 |
| x |
因为
| a2 |
| x |
| 2 |
| ||
| 2 |
| ||
| 2 |
| a |
| 2 |
所以(S△ADP)max=
| a2 |
| 4 |
| 2 |
| ||
| 2 |
答:当矩形的长为
| ||
| 2 |
点评:本题考查的知识点是函数模型的选择与应用,基本不等式,其中(1)中根据已知条件判断出tan2α=tan∠APD=
,是解答的关键,而(2)中关键是求出绿化面积S△ADP=
AD•DP=
(3a-
-2x)的表达式,为基本不等式的使用创造条件.
| AD |
| DP |
| 1 |
| 2 |
| a |
| 4 |
| a2 |
| x |

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 某居民小区内建有一块矩形草坪ABCD,AB=50米,BC=
某居民小区内建有一块矩形草坪ABCD,AB=50米,BC=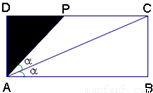
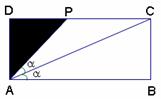 (1)求线段
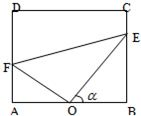
(1)求线段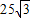 米,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设三条小路OE、EF和OF,考虑到小区整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°,如图所示.
米,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设三条小路OE、EF和OF,考虑到小区整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°,如图所示.