题目内容
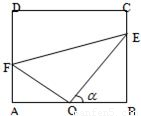
某居民小区内建有一块矩形草坪ABCD,AB=50米,BC=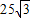 米,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设三条小路OE、EF和OF,考虑到小区整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°,如图所示.
米,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设三条小路OE、EF和OF,考虑到小区整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°,如图所示.(1)设∠BOE=α,试将△OEF的周长l表示成α的函数关系式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为400元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
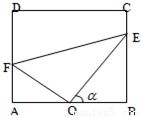
【答案】分析:(1)要将△OEF的周长l表示成α的函数关系式,需把△OEF的三边分别用含有α的关系式来表示,而OE,
OF,分别可以在Rt△OBE,Rt△OAF中求解,利用勾股定理可求EF,从而可求.
(2)要求铺路总费用最低,只要求△OEF的周长l的最小值即可.由(1)得, ,
,
利用换元,设sinα+cosα=t,则 ,从而转化为求函数在闭区间上的最小值.
,从而转化为求函数在闭区间上的最小值.
解答:解:(1)∵在Rt△BOE中,OB=25,∠B=90°,∠BOE=α,
∴OE=
在Rt△AOF中,OA=25,∠A=90°,∠AFO=α,
∴OF= .
.
又∠EOF=90°,
∴EF═ =
= ,
,
∴
即 .
.
当点F在点D时,这时角α最小,求得此时α= ;
;
当点E在C点时,这时角α最大,求得此时α= .
.
故此函数的定义域为
(2)由题意知,要求铺路总费用最低,只要求△OEF的周长l的最小值即可.
由(1)得, ,
,
设sinα+cosα=t,则 ,
,
∴
由t=sinα+cosα= ,又
,又 ,得
,得 ,
,
∴ ,
,
从而 ,当
,当 ,即BE=25时,
,即BE=25时, ,
,
所以当BE=AF=25米时,铺路总费用最低,最低总费用为 元.
元.
点评:本题主要考查了借助于三角函数解三角形在实际问题中的应用,考查了利用数学知识解决实际问题的能力,及推理运算的能力.
OF,分别可以在Rt△OBE,Rt△OAF中求解,利用勾股定理可求EF,从而可求.
(2)要求铺路总费用最低,只要求△OEF的周长l的最小值即可.由(1)得,
 ,
,
利用换元,设sinα+cosα=t,则
 ,从而转化为求函数在闭区间上的最小值.
,从而转化为求函数在闭区间上的最小值.解答:解:(1)∵在Rt△BOE中,OB=25,∠B=90°,∠BOE=α,
∴OE=

在Rt△AOF中,OA=25,∠A=90°,∠AFO=α,
∴OF=
 .
.又∠EOF=90°,
∴EF═
 =
= ,
,∴

即
 .
.当点F在点D时,这时角α最小,求得此时α=
 ;
;当点E在C点时,这时角α最大,求得此时α=
 .
.故此函数的定义域为

(2)由题意知,要求铺路总费用最低,只要求△OEF的周长l的最小值即可.
由(1)得,
 ,
,
设sinα+cosα=t,则
 ,
,∴

由t=sinα+cosα=
 ,又
,又 ,得
,得 ,
,∴
 ,
,从而
 ,当
,当 ,即BE=25时,
,即BE=25时, ,
,所以当BE=AF=25米时,铺路总费用最低,最低总费用为
 元.
元.点评:本题主要考查了借助于三角函数解三角形在实际问题中的应用,考查了利用数学知识解决实际问题的能力,及推理运算的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
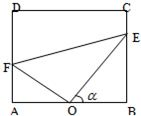 某居民小区内建有一块矩形草坪ABCD,AB=50米,BC=
某居民小区内建有一块矩形草坪ABCD,AB=50米,BC=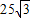 米,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设三条小路OE、EF和OF,考虑到小区整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°,如图所示.
米,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设三条小路OE、EF和OF,考虑到小区整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°,如图所示.