题目内容
【题目】设![]() .
.
(1)求证:![]() 在区间
在区间![]() 上没有零点;
上没有零点;
(2)若不等式![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用导数可求得![]() 在
在![]() 上是增函数,可得
上是增函数,可得![]() ,由此得到结论;
,由此得到结论;
(2)解法一:利用放缩的方式可知![]() ,则只需
,则只需![]() 即可;利用导数可证得
即可;利用导数可证得![]() ,由
,由![]() 时,
时,![]() 可确定此时满足题意;由
可确定此时满足题意;由![]() 时,存在实数
时,存在实数![]() ,使得任意
,使得任意![]() ,均有
,均有![]() ,可知存在
,可知存在![]() ,不满足题意;
,不满足题意;
解法二:构造函数![]() ,求导后,分别在
,求导后,分别在![]() 和
和![]() 两种情况下根据导函数的符号确定函数单调性,由此可确定
两种情况下根据导函数的符号确定函数单调性,由此可确定![]() 符合题意.
符合题意.
(1)![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() 为增函数,
为增函数,![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数,![]() ,
,
![]() 在区间
在区间![]() 上没有零点;
上没有零点;
(2)解法一:由(1)知:当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上为增函数,
上为增函数,![]() ,即
,即![]() ,
,
![]() 在
在![]() 上为增函数,
上为增函数,![]() ,即
,即![]() ,
,
所以![]() 对任意的
对任意的![]() 恒成立.
恒成立.
又![]() ,
,![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() 对任意的
对任意的![]() 恒成立;
恒成立;
当![]() 时,设
时,设![]() ,则
,则![]() ,
,
![]() ,所以存在实数
,所以存在实数![]() ,使得任意
,使得任意![]() ,均有
,均有![]() ,
,
所以![]() 在
在![]() 上为减函数,
上为减函数,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 时不符合题意;
时不符合题意;
综上所述:实数![]() 的取值范围为
的取值范围为![]() .
.
解法二:![]() 等价于
等价于![]()
设![]() ,则
,则![]() ,
,
设![]() ,则
,则
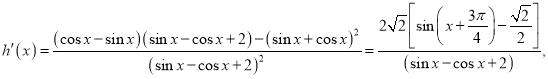
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
![]() 当
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
![]() ,
,
所以当![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,即
,即![]() ,即
,即![]()
所以当![]() 时,
时,![]() 对任意
对任意![]() 恒成立.
恒成立.
当![]() 时,
时,![]() ,
,![]() 存在
存在![]() ,当
,当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上是减函数,
上是减函数,![]() 当
当![]() 时,
时,![]() ,
,
即![]() ,不符合题意,故
,不符合题意,故![]() 不满足题意,
不满足题意,
综上所述,![]() 的取值范围是
的取值范围是![]() .
.

【题目】东莞的轻轨给市民出行带来了很大的方便,越来越多的市民选择乘坐轻轨出行,很多市民都会开汽车到离家最近的轻轨站,将车停放在轻轨站停车场,然后进站乘轻轨出行,这给轻轨站停车场带来很大的压力.某轻轨站停车场为了解决这个问题,决定对机动车停车施行收费制度,收费标准如下:4小时内(含4小时)每辆每次收费5元;超过4小时不超过6小时,每增加一小时收费增加3元;超过6小时不超过8小时,每增加一小时收费增加4元,超过8小时至24小时内(含24小时)收费30元;超过24小时,按前述标准重新计费.上述标准不足一小时的按一小时计费.为了调查该停车场一天的收费情况,现统计1000辆车的停留时间(假设每辆车一天内在该停车场仅停车一次),得到下面的频数分布表:
|
|
|
|
|
|
|
频数(车次) | 100 | 100 | 200 | 200 | 350 | 50 |
以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率.
(1)现在用分层抽样的方法从上面1000辆车中抽取了100辆车进行进一步深入调研,记录并统计了停车时长与司机性别的![]() 列联表:
列联表:
男 | 女 | 合计 | |
不超过6小时 | 30 | ||
6小时以上 | 20 | ||
合计 | 100 |
完成上述列联表,并判断能否有90%的把握认为“停车是否超过6小时”与性别有关?
(2)(i)![]() 表示某辆车一天之内(含一天)在该停车场停车一次所交费用,求
表示某辆车一天之内(含一天)在该停车场停车一次所交费用,求![]() 的概率分布列及期望
的概率分布列及期望![]() ;
;
(ii)现随机抽取该停车场内停放的3辆车,![]() 表示3辆车中停车费用大于
表示3辆车中停车费用大于![]() 的车辆数,求
的车辆数,求![]() 的概率.
的概率.
参考公式: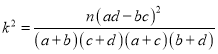 ,其中
,其中![]()
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 2.072 | 2.706 | 3.841 | 5.024 |
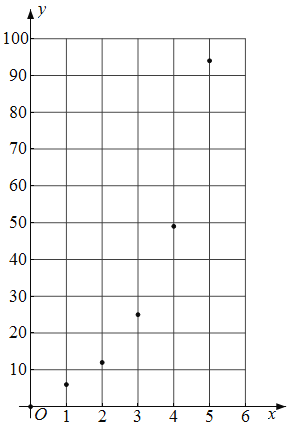
【题目】某种昆虫的日产卵数和时间变化有关,现收集了该昆虫第1天到第5天的日产卵数据:
第x天 | 1 | 2 | 3 | 4 | 5 |
日产卵数y(个) | 6 | 12 | 25 | 49 | 95 |
对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
|
|
|
|
15 | 55 | 15.94 | 54.75 |
(1)根据散点图,利用计算机模拟出该种昆虫日产卵数y关于x的回归方程为![]() (其中e为自然对数的底数),求实数a,b的值(精确到0.1);
(其中e为自然对数的底数),求实数a,b的值(精确到0.1);
(2)根据某项指标测定,若日产卵数在区间(e6,e8)上的时段为优质产卵期,利用(1)的结论,估计在第6天到第10天中任取两天,其中恰有1天为优质产卵期的概率.
附:对于一组数据(v1,μ1),(v2,μ2),…,(vn,μn),其回归直线的斜率和截距的最小二乘估计分别为![]() ,
,![]() .
.