题目内容
5．某校选修乒乓球课程的学生中，高一年级有30名，高二年级有40名，现从这70人中用分层抽样的方法抽取一个容量为14的样本，则在高二年级的学生中应抽取的人数为（ ）| A． | 6 | B． | 8 | C． | 10 | D． | 12 |
分析 根据总人数和抽取的人数，做出每个个体被抽到的概率，利用这个概率乘以高二的学生数，得到高二要抽取的人数．
解答 解：∵高一年级有30名，高二年级有40名，这70人中用分层抽样的方法抽取一个容量为14的样本
故每个个体被抽到的概率是$\frac{14}{70}$=$\frac{1}{5}$
∵高二年级有40名，
∴要抽取40×$\frac{1}{5}$=8，
故选：B．
点评 本题考查分层抽样，在分层抽样过程中每个个体被抽到的概率相等，这是解题的依据，本题是一个基础题．
练习册系列答案
阅读快车系列答案
相关题目
20．已知数列{an}的前n项和为${S_n}={n^2}-2n$，则a3+a17=（ ）
| A． | 36 | B． | 35 | C． | 34 | D． | 33 |
17．已知集合A={-1，1}，B={x|x∈R，1≤2x≤4}，则A∩B等于（ ）
| A． | {0，1} | B． | {-1，1} | C． | {1} | D． | {-1，0，1} |
14．对变量x，y有观测数据（xi，yi）（i=1，2，3，4，5），得表1；对变量u，v有观测数据（ui，vi）（i=1，2，3，4，5），得表2．由这两个表可以判断（ ）
表1：
表2：
表1：
| x | 1 | 2 | 3 | 4 | 5 |
| y | 2.9 | 3.3 | 3.6 | 4.4 | 5.1 |
| u | 1 | 2 | 3 | 4 | 5 |
| v | 25 | 20 | 21 | 15 | 13 |
| A． | 变量x与y正相关，u与v正相关 | B． | 变量x与y负相关，u与v正相关 | ||
| C． | 变量x与y负相关，u与v负相关 | D． | 变量x与y正相关，u与v负相关 |
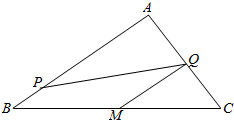如图，在Rt△ABC中，AB=4，AC=3，∠A=90°，$\overrightarrow{AP}$=m$\overrightarrow{PB}$，$\overrightarrow{AQ}$=n$\overrightarrow{QC}$，m，n＞0，且满足$\frac{1}{m}$+$\frac{1}{n}$=$\frac{1}{2}$，M是BC的中点，对任意的λ∈R，|λ•$\overrightarrow{QP}$+$\overrightarrow{QM}$|的最小值记为f（m），则对任意m＞0，f（m）的最大值为$\frac{1}{2}$．