题目内容
设x,y满足约束条件:
且z=x-ay的最小值为7,则a= .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:由题意易得最小值在点(-
,
)处取到,代值解a验证可得.
| a+1 |
| 2 |
| -a+1 |
| 2 |
解答:
解:不等式组
所对应的可行域为两直线相交所称的角形区域,
联立
,可解得
,故最小值在点(-
,
)处取到,
∴-
-a•
=7,解得a=-3或5,
经验证当a=5时,目标函数取最大值,不合题意
故答案为:-3
|
联立
|
|
| a+1 |
| 2 |
| -a+1 |
| 2 |
∴-
| a+1 |
| 2 |
| -a+1 |
| 2 |
经验证当a=5时,目标函数取最大值,不合题意
故答案为:-3
点评:本题考查简单线性规划,涉及分类讨论的思想,属中档题.

练习册系列答案
相关题目
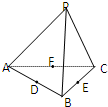 空间四边形PABC的各边及对角线长度都相等,D、E、F分别是AB、BC、CA的中点,下列四个结论中不成立的是( )
空间四边形PABC的各边及对角线长度都相等,D、E、F分别是AB、BC、CA的中点,下列四个结论中不成立的是( )| A、DF∥平面PBC |
| B、AB⊥平面PDC |
| C、平面PEF⊥平面ABC |
| D、平面PAE平面PBC |
 四棱锥P-ABCD中,底面ABCD是边长为8的菱形,∠BAD=
四棱锥P-ABCD中,底面ABCD是边长为8的菱形,∠BAD=