题目内容
函数y=f(x)在(-2,0)上是减函数,函数y=f(x-2)是偶函数,则( )
A、f(-
| ||||||
B、f(-
| ||||||
C、f(-
| ||||||
D、f(-
|
分析:函数y=f(x-2)是偶函数,可得出函数关于x=-2对称,又函数y=f(x)在(-2,0)上是减函数可得出函数在(-4,-2)是一增函数,即得出自变量离x=-2的距离越近,函数值越大,由此规律比较大小选出正确选项即可
解答:解:∵函数y=f(x)在(-2,0)上是减函数,函数y=f(x-2)是偶函数
∴函数关于x=-2对称,数在(-4,-2)是一增函数,
∴自变量离x=-2的距离越近,函数值越大,
由于-
,-
,-
都在(-4,0)上,且|-
+2|>|-
+2|>|-
+2|
∴f(-
)<f(-
)<f(-
)
故选C
∴函数关于x=-2对称,数在(-4,-2)是一增函数,
∴自变量离x=-2的距离越近,函数值越大,
由于-
| 10 |
| 3 |
| 4 |
| 3 |
| 7 |
| 3 |
| 10 |
| 3 |
| 4 |
| 3 |
| 7 |
| 3 |
∴f(-
| 10 |
| 3 |
| 4 |
| 3 |
| 7 |
| 3 |
故选C
点评:本题考查奇偶性与单调性的综合,解题的关键是根据题设条件判断出函数的性质自变量离x=-2的距离越近,函数值越大,利用此规律比较三个函数值的大小,本题考查了推理论证的能力.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
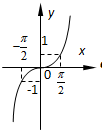 已知函数y=f(x)的图象如图,则函数
已知函数y=f(x)的图象如图,则函数