题目内容
定义在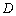 上的函数
上的函数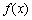 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数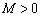 ,都有
,都有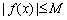 成立,则称
成立,则称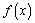 是
是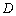 上的有界函数,其中
上的有界函数,其中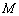 称为函数
称为函数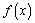 的上界.
的上界.
已知函数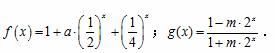
(1)当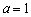 时,求函数
时,求函数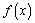 在
在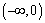 上的值域,并判断函数
上的值域,并判断函数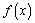 在
在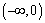 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数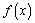 在
在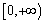 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数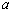 的取值范围;
的取值范围;
(3)若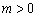 ,函数
,函数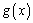 在
在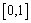 上的上界是
上的上界是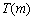 ,求
,求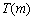 的取值范围.
的取值范围.
(1)当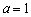 时,
时,
∵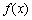 在
在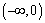 上
上 递减,∴
递减,∴ ,即
,即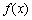 在
在 的值域为
的值域为 ,
,
故不存在常数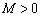 ,使
,使
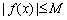 成立,∴函数
成立,∴函数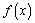 在
在 上不是有界函数.
上不是有界函数.
 设
设 ,
, ,
, ,由
,由
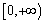 得
得 ,
,
∴ 在
在 上递减,
上递减, 在
在 上递增,
上递增, 在
在 上的最大值为
上的最大值为 ,
, 在
在 上的最小值为
上的最小值为 ,∴实数
,∴实数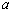 的取值范围为
的取值范围为 .
.


练习册系列答案
相关题目
 的系数,如果抛物线经过原点,且顶点在第一象限,则这样的抛物线共有多少条?
的系数,如果抛物线经过原点,且顶点在第一象限,则这样的抛物线共有多少条? 方程
方程 有两个不相等负数根;命题
有两个不相等负数根;命题 方程
方程 无实数根.若命题“
无实数根.若命题“ 或
或 ”是真命题,则实数
”是真命题,则实数 的取值范围是 .
的取值范围是 . 且
且 是奇函数.
是奇函数. 时,
时, ,求
,求 ,
, .若“
.若“ ”是“
”是“ ”的必要条件,则实数
”的必要条件,则实数 的范围是________.
的范围是________.
 的k(k∈N*)
的k(k∈N*) 叫作“简易数”.则在[1,2 012]内所有“简易数”的和为________.
叫作“简易数”.则在[1,2 012]内所有“简易数”的和为________. 的左,右焦点分别为
的左,右焦点分别为 ,焦距为2c,若直线
,焦距为2c,若直线 与椭圆C的一个交点M满足
与椭圆C的一个交点M满足 ,则该椭圆的离心率等于__________.
,则该椭圆的离心率等于__________.