题目内容
从{-3,-2,-1,0,1,2,3}中,任取3个不同的数作为抛物线方程y=ax2+bx+c 的系数,如果抛物线经过原点,且顶点在第一象限,则这样的抛物线共有多少条?
的系数,如果抛物线经过原点,且顶点在第一象限,则这样的抛物线共有多少条?
解 因为抛物线经过原点,所以c=0,从而知c只有1种取值.
又抛物线y=ax2+bx+c顶点在第一象限,所以顶点坐标满足
由c=0解得a<0,b>0,
所以a∈{-3,-2,-1},b∈{1,2,3},
这样要求的抛物线的 条数可由a,b,c的取值来确定:
条数可由a,b,c的取值来确定:
第一步:确定a的值,有3种方法;
第二步:确定b的值,有3种方法;
第三步:确定c的值,有1种方法.
由分步计数原理知,表示的不同的抛物线有N=3×3×1=9(条).


练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 少1人参加.
少1人参加. 展开式中的倒数第三项的系数为45,求:
展开式中的倒数第三项的系数为45,求: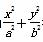 =1(a>b>0),a∈{1,2,3,4,5,6,7},b∈{1,2,3,4,5},这样的椭圆共有多少个?
=1(a>b>0),a∈{1,2,3,4,5,6,7},b∈{1,2,3,4,5},这样的椭圆共有多少个? 且b0+b1+b2+…+bn=30,则自然数n的值为________.
且b0+b1+b2+…+bn=30,则自然数n的值为________. 的展开式的前三项系数的和为129,试问这个展开式中是否有常数项?有理项?如果没有,请说明理由;如果有,求出这一项.
的展开式的前三项系数的和为129,试问这个展开式中是否有常数项?有理项?如果没有,请说明理由;如果有,求出这一项. ,且与直线
,且与直线 相切于点
相切于点 的圆的方程是______.
的圆的方程是______.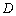 上的函数
上的函数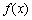 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数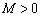 ,都有
,都有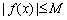 成立,则称
成立,则称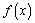 是
是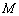 称为函数
称为函数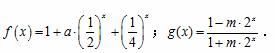
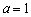 时,求函数
时,求函数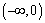 上的值域,并判断函数
上的值域,并判断函数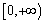 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数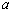 的取值范围;
的取值范围;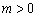 ,函数
,函数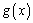 在
在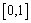 上的上界是
上的上界是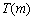 ,求
,求