题目内容
已知数列{an}满足a1=1,an=logn(n+1)(n≥2,n∈N*).定义:使乘积a1·a2·…·ak为正整数 的k(k∈N*)
的k(k∈N*) 叫作“简易数”.则在[1,2 012]内所有“简易数”的和为________.
叫作“简易数”.则在[1,2 012]内所有“简易数”的和为________.
【答案】
[解析]∵an=logn(n+1)= ,∴a1·a2·…·ak=1·
,∴a1·a2·…·ak=1· ·
· ·…·
·…· =
= =log2(k+1),
=log2(k+1),
则“简易数”k使log2(k+1)为整数,即满足2n=k+1,所以 k=2n-
k=2n- 1,则在[1,2 012
1,则在[1,2 012 ]内所有“简易数”的和为21-1+2
]内所有“简易数”的和为21-1+2 2-1+…+210-1=
2-1+…+210-1= -10=1 023×2-10=2 036.
-10=1 023×2-10=2 036.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 ,且与直线
,且与直线 相切于点
相切于点 的圆的方程是______.
的圆的方程是______.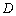 上的函数
上的函数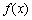 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数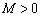 ,都有
,都有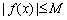 成立,则称
成立,则称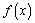 是
是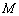 称为函数
称为函数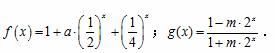
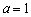 时,求函数
时,求函数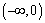 上的值域,并判断函数
上的值域,并判断函数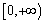 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数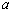 的取值范围;
的取值范围;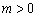 ,函数
,函数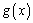 在
在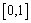 上的上界是
上的上界是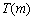 ,求
,求 =1,其中m、n∈{1,2,3,4,5,6},如果事件A为“方程
=1,其中m、n∈{1,2,3,4,5,6},如果事件A为“方程
 是三个不同的平面,命题“
是三个不同的平面,命题“ ”是真命题.
”是真命题. 保持不变,在所得的所有新命题中,真命题
保持不变,在所得的所有新命题中,真命题  中,
中, ,
, ,则四棱锥
,则四棱锥 的体积为 cm3.
的体积为 cm3.
 ,直线
,直线 斜率存在且过点
斜率存在且过点 ,若
,若 相交,则l的斜率k的取值范围是 .
相交,则l的斜率k的取值范围是 . ,其中
,其中 成公比为
成公比为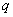 的等比数列,
的等比数列, 成公差为1的等差数列,则
成公差为1的等差数列,则