题目内容
11．已知集合A={x|ax2+x+1=0}中至少有一个元素，求实数a的取值范围．分析 A中至少有一个元素?ax2+x+1=0至少有一个解，a=0，或△≥0，解出即可．
解答 解：A中至少有一个元素?ax2+x+1=0至少有一个解．
∴a=0，或a≠0，△=1-4a≥0，
解得a≤$\frac{1}{4}$且a≠0．
综上所述，实数a的取值范围是（-∞，$\frac{1}{4}$]．
点评 本题考查了一元二次的实数根与判别式的关系、集合的性质，考查了推理能力、计算能力，属于中档题．
练习册系列答案
相关题目
19．当x=$\frac{π}{4}$时，函数f（x）=sin（x+φ）取得最小值，则函数y=f（$\frac{3π}{4}$-x）的一个单调递增区间是（ ）
| A． | （0，$\frac{π}{2}$） | B． | （$\frac{π}{2}$，π） | C． | （-$\frac{π}{2}$，-$\frac{π}{4}$） | D． | （$\frac{3π}{2}$，2π） |
16．已知集合M={$\frac{1}{2}$，1，2，3，4}，N={y|y=log2x，x∈M}，则M∩N是（ ）
| A． | {1，2} | B． | {1，4} | C． | {1} | D． | {2} |
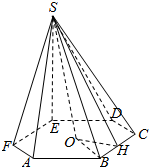正六棱锥的底面周长为24，斜高SH与高SO所成的角为30°．