题目内容
4.(Ⅰ)计算:(log29)•(log34)-(2$\sqrt{2}$)${\;}^{\frac{2}{3}}$-eln2;(Ⅱ)化简:$\frac{\sqrt{1-sin20°}}{cos10°-sin170°}$.
分析 (Ⅰ)根据对数的基本运算和指数幂的运用法则求解即可,
(Ⅱ)根据二倍角和同角三角函数公式化简即可.
解答 解:(Ⅰ)(log29)•(log34)-(2$\sqrt{2}$)${\;}^{\frac{2}{3}}$-eln2;
原式=2log23•(2log32)-$(2×{2}^{\frac{1}{2}})^{\frac{2}{3}}$-2
=2×2-$({2}^{\frac{3}{2}})^{\frac{2}{3}}$-2
=4-2-2
=0.
(Ⅱ)化简:$\frac{\sqrt{1-sin20°}}{cos10°-sin170°}$.
原式=$\frac{\sqrt{si{n}^{2}10°+co{s}^{2}10°-2sin10°cos10°}}{cos10°-sin10°}$=$\frac{cos10°-sin10°}{cos10°-sin10°}=1$
点评 本题主要考察了对数的基本运算和指数幂的运用法以及二倍角和同角三角函数公式化简能力.

练习册系列答案
相关题目
15.已知两个正数a,b满足3a+2b=1,则$\frac{3}{a}$+$\frac{2}{b}$的最小值是( )
| A. | 23 | B. | 24 | C. | 25 | D. | 26 |
19.sin$\frac{2017π}{3}$的值等于( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $-\frac{\sqrt{3}}{2}$ |
9.若复数$\frac{1-bi}{2+i}$=$\frac{1}{2}$(i是虚数单位,b是实数),则b=( )
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
16.某程序框图如图所示,该程序运行后输出S的值是( )


| A. | 22 | B. | 25 | C. | 28 | D. | 31 |
14.设向量$\overrightarrow{a}$=(1,7),$\overrightarrow{b}$=(-3,4),则向量$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影是( )
| A. | 5$\sqrt{2}$ | B. | $\frac{5\sqrt{2}}{2}$ | C. | 5 | D. | -5 |
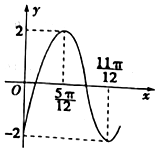 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.