题目内容
已知直线l: kx-y+1+2k=0(k∈R).
(1)证明:直线l过定点;
(2)若直线不经过第四象限,求k的取值范围;
(3)若直线l交x轴负半轴于A,交y轴正半轴于B,△AOB的面积为S,求S的最小值并求此时直线l的方程.
[解析] (1)直线l的方程是:k(x+2)+(1-y)=0,令
∴无论k取何值,直线总经过定点(-2,1).
(2)由方程知,直线在x轴上的截距为- (k≠0),在y轴上的截距为1+2k,要使直线不经过第四象限,则必须有
(k≠0),在y轴上的截距为1+2k,要使直线不经过第四象限,则必须有
 或k=0,解之得k≥0.
或k=0,解之得k≥0.
 ≥
≥ (2×2+4)=4,
(2×2+4)=4,
“=”成立的条件是k>0且4k= ,即k=
,即k= ,
,
∴Smin=4,此时l:x-2y+4=0.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
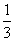 B.
B.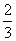
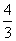
 B.
B.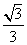
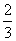 D.
D.


 )2=1
)2=1 )2+(y-1)2=1
)2+(y-1)2=1 为实数,命题甲:
为实数,命题甲: ,命题乙:
,命题乙: ,则命题甲是命题乙的( )
,则命题甲是命题乙的( ) ,
, ,
, ,那么a等于
,那么a等于