题目内容
9.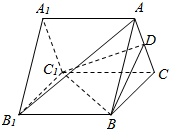 如图所示,已知A1B1C1-ABC是正三棱柱(底面是正三角形,侧棱与底面垂直),D是AC的中点.
如图所示,已知A1B1C1-ABC是正三棱柱(底面是正三角形,侧棱与底面垂直),D是AC的中点. (1)证明:AB1∥平面DBC1;
(2)若BB1=8,BC=6,求异面直线BD与AB1所成角的余弦值.
分析 (1)可连接B1C,设交BC1于点E,并连接DE,从而可说明DE∥AB1,这样根据线面平行的判定定理即可得出AB1∥平面DBC1;
(2)根据上面便知,∠EDB为异面直线BD与AB1所成角,根据三棱柱为正三棱柱,由BB1=8,BC=6便可求出BD,BE,AB1的长,而由DE为△AB1C的中位线便可求出DE,这样在△BDE中,根据余弦定理即可求出cos∠EDB,即求出异面直线BD与AB1所成角的余弦值.
解答  解:(1)证明:如图,连接B1C,交BC1于点E,连接DE;
解:(1)证明:如图,连接B1C,交BC1于点E,连接DE;
∵D是AC中点,E是B1C中点;
∴DE∥AB1,且$DE=\frac{1}{2}A{B}_{1}$;
又DE?平面DBC1,AB1?平面DBC1;
∴AB1∥平面DBC1;
(2)∵AB1∥DE;
∴∠EDB是异面直线BD与AB1所成角;
∵BB1=8,BC=6,三棱柱A1B1C1-ABC为正三棱柱;
∴$BE=5,A{B}_{1}=10,BD=3\sqrt{3}$,$DE=\frac{1}{2}A{B}_{1}=5$;
∴在△BDE中,由余弦定理得:cos∠EDB=$\frac{B{D}^{2}+D{E}^{2}-B{E}^{2}}{2BD•DE}=\frac{27}{30\sqrt{3}}=\frac{3\sqrt{3}}{10}$;
即异面直线BD与AB1所成角的余弦值为$\frac{3\sqrt{3}}{10}$.
点评 考查正三棱柱的定义,三角形中位线的性质,线面平行的判定定理,以及异面直线所成角的概念及求法,余弦定理.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
4.在△ABC中,点D,E分别是边AB,AC上的-点,且满足AD=$\frac{1}{3}$AB,AE=$\frac{1}{3}$AC,若CD⊥BE,则cosA的最小值是( )
| A. | $\frac{3}{5}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{4}{5}$ | D. | $\frac{\sqrt{2}}{2}$ |