题目内容

如果有底的圆柱底面直径和高都等于球的直径，则圆柱与球的表面积之比为（　　）
A、3：2B、3：1
C、2：1D、2：1
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：设球的半径为r，则 S圆柱：S球=[2πr2+（2r）•2πr]：4πr2，可得结论．
解答： 解：设球的半径为r，则 S圆柱：S球=[2πr2+（2r）•2πr]：4πr2=3：2．
故选：A．
点评：本题考查几何体的表面积，考查计算能力，是基础题．
练习册系列答案
相关题目
函数y=lg（-1+2x）的定义域是
 
．
已知集合A={x|x2+3x+2≥0}，B={x|mx2-4x+m-1＞0，m∈R}，若A∩B=∅，且A∪B=A，求m的取值范围．
已知A（3，1），B（-1，2）若∠ACB的平分线方程为y=x+1，则AC所在的直线方程为（　　）
A、y=2x+4
B、y=
1
2
x-3
C、x-2y-1=0
D、3x+y+1=0
炼钢是一个氧化降碳的过程，钢水含碳量的多少直接影响冶炼时间的长短，必须掌握钢水含碳量和冶炼时间的关系．如果已测得炉料溶化完毕时钢水的含碳量x与冶炼时间y（从炉料溶化完毕到出钢的时间）的一列数据，如表所示：
x（0.01%）104180190177147134150191204121
y/min100200210185155135170205235125
（1）y与x是否具有线性相关关系？
（2）如果y与x具有线性相关关系，求出回归直线方程．
（3）预报当钢水含碳量为160个0.01%时，应冶炼多少分钟？
数列{an}中，对任意的m，n，p∈N+，当m+n=p时，都有am•an=ap，若a1=
1
2
，则a10的值为
 
．
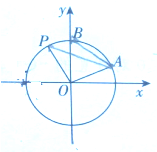如图，一个半径为R的圆上一点A（
3
，1），动点P从点A出发，沿圆周逆时针方向匀速运动，设t时刻时，P点坐标为（x（t），y（t）），其中t∈[2，6]时，y（t）单调递减，且y（6）=y（10），则0≤t≤10时，数量积
AP
•
AB
的最大值为（　　）
A、4B、6C、10D、12
某厂生产某种产品，总成本Y（单位：万元）与总产量x（单位：千台）之间的函数关系为Y（x）=2+x，销售总收入T（单位：万元）与总产量x（单位：千台）之间的函数关系为T（x）=4x-
1
2
x2．那么，该厂年产多少台时总利润最大？最大总利润是多少？
已知线段AB的长为3，平面上一动点M到点A的距离是到点B的距离的2倍，则动点M的轨迹方程为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网