题目内容

在△ABC中，角A，B，C的对边分别为a，b，c，若b=2，c=3，△ABC的面积为2，则sinA=
 
．
考点：正弦定理
专题：计算题,解三角形
分析：由三角形的面积公式S△ABC=
1
2
bcsinA，代入数据计算即可得到sinA．
解答： 解：由于b=2，c=3，△ABC的面积为2，
则S△ABC=
1
2
bcsinA=2，
即有sinA=
4
bc
=
4
2×3
=
2
3
．
故答案为：
2
3
．
点评：本题考查三角形的面积公式及运用，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率e=
3
2
，点P(
3
，
1
2
)在椭圆C上．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点Q（2，0），作两条互相垂直的动直线QA、QB，分别交椭圆C于 A、B两点，求证：直线AB必过定点，并求出该定点坐标．
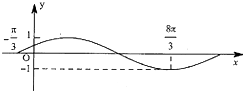将函数y=sinx图象上点的横坐标扩大到原来的m倍，纵坐标保持不变，再向左平移n个单位得到如图所示函数的图象，则m，n可以为（　　）
A、m=2，n=
π
3
B、m=2，n=
11π
3
C、m=4，n=
π
3
D、m=4，n=
11π
3
在△ABC中，三个角A，B，C的对边边长分别为a=3，b=4，c=6，则bccosA的值为
 
．
在等分区间的情况下，f（x）=
1
1+x2
（x∈[0，2]）及x轴所围成的曲边梯形的面积和式的极限形式正确的是（　　）
A、
lim
n→+∞
n
i=1
[
1
1+(
i
n
)2
•
2
n
]
B、
lim
n→+∞
n
i=1
[
1
1+(
2i
n
)2
•
2
n
]
C、
lim
n→+∞
n
i=1
[
1
1+i2
•
1
n
]
D、
lim
n→+∞
n
i=1
[
1
1+(
i
n
)2
•
1
n
]
在△ABC中，已知sinA=
1
5
，sinB=
1
10
则其最长边与最短边的比为
 
．
已知在△A BC中，角 A，B，C所对的边分别为a，b，c．已知c=2，sinA-cos（A-
π
6
）=cos（B-C+
π
6
）．
（Ⅰ）求角C的大小；
（Ⅱ）若sinA=
1
3
，求边b的长．
已知随机变量ξ服从正态分布N（2，δ2），p（ξ＜4）=0.84，则P（2＜ξ＜4）=（　　）
A、0.68B、0.34
C、0.17D、0.16
若k∈R，则“-3＜k＜3”是“方程
x2
k-3
-
y2
k+3
=1表示双曲线”的（　　）
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网