题目内容
已知双曲线的中心在原点O,右焦点为F(c,0),P是双曲线右支上一点,且△OFP的面积为(1)若点P的坐标为(2,![]() ),求此双曲线的离心率;
),求此双曲线的离心率;
(2)若![]() =(
=(![]() -1)c2,当|
-1)c2,当|![]() |取得最小值时,求此双曲线的方程.
|取得最小值时,求此双曲线的方程.
答案:解:(1)设所求的双曲线的方程为![]() =1(a>0,b>0),
=1(a>0,b>0),
则![]() |OF|×
|OF|×![]() =
=![]() ,∴c=
,∴c=![]() .
.
∴b2=c2-a2=2-a2.
由点P(2,![]() )在双曲线上,∴
)在双曲线上,∴![]() =1,解得a2=1.
=1,解得a2=1.
∴离心率e=![]() =
=![]() .
.
(2)设所求的双曲线的方程为![]() =1(a>0,b>0),P(x1,y1),
=1(a>0,b>0),P(x1,y1),
则![]() =(x1-c,y1).
=(x1-c,y1).
∵△OFP的面积为![]() ,∴
,∴![]() |
|![]() ||y1|=
||y1|=![]() .∴|y1|=
.∴|y1|=![]() .
.
∵![]() =(
=(![]() -1)c2,∴
-1)c2,∴![]() =(x1-c)c=(
=(x1-c)c=(![]() -1)c2.解得x1=
-1)c2.解得x1=![]() c.
c.
∵|![]() |=
|=![]() ≥4,
≥4,
当且仅当c=![]() 时等号成立.
时等号成立.
此时P(![]() ,±
,±![]() ).由此得
).由此得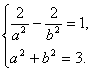 解得
解得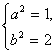 或
或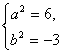 (舍去).
(舍去).
故所求双曲线的方程为x2![]() =1.
=1.

练习册系列答案
相关题目

 ,求此双曲线的离心率;
,求此双曲线的离心率; ,当
,当 取得最小值时,求此双曲线的方程.
取得最小值时,求此双曲线的方程.
 ,求此双曲线的离心率;
,求此双曲线的离心率; ,当
,当 取得最小值时,求此双曲线的方程.
取得最小值时,求此双曲线的方程.