题目内容
11.已知集合A={(x,y)|y=|x2-1|},B={(x,y)|y=$\sqrt{1-{x}^{2}}$},求A∩B的真子集个数.分析 由A中y=|x2-1|,利用绝对值的代数意义化简得到y=x2-1或y=-x2+1,分别与B中y=$\sqrt{1-{x}^{2}}$联立求出x与y的值,确定出A∩B的交集,即可求出交集的真子集个数.
解答 解:由A中y=|x2-1|,
得到y=x2-1或y=-x2+1,
若y=x2-1时,与y=$\sqrt{1-{x}^{2}}$联立得:$\left\{\begin{array}{l}{y={x}^{2}-1}\\{y=\sqrt{1-{x}^{2}}}\end{array}\right.$,
解得:x=±1,y=0(负值舍去),
若y=-x2+1,与y=$\sqrt{1-{x}^{2}}$联立得:$\left\{\begin{array}{l}{y=-{x}^{2}+1}\\{y=\sqrt{1-{x}^{2}}}\end{array}\right.$,
解得:x=0,y=1,
则A∩B={(1,0),(-1,0),(0,1)},即真子集个数为23-1=7个.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 ,若对任意
,若对任意 都有
都有 成立,则( )
成立,则( ) B.
B. C.
C. D.
D.
 中,
中, ,且数列
,且数列 是等比数列,则
是等比数列,则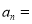 ___________.
___________.