题目内容
6.已知函数f(x)=A(sin$\frac{x}{2}$cosφ+cos$\frac{x}{2}$sinφ)(A>0,0<φ<π)的最大值是2,且f(0)=2.(1)求φ的值;(2)已知锐角△ABC的三个内角分别为∠A、∠B、∠C,若f(2A)=$\frac{6}{5}$,f(2B+π)=-$\frac{24}{13}$,求f(2C).
分析 (1)由两角和的正弦公式化简解析式可得f(x)=Asin($\frac{x}{2}+$φ),由函数的最大值是2可求A,由f(0)=2sinφ=2,结合φ的范围可求φ的值.
(2)由(1)可得f(x)=2sin($\frac{x}{2}+$$\frac{π}{2}$),由f(2A)=2sin(A+$\frac{π}{2}$)=$\frac{6}{5}$,可得cosA,由f(2B+π)=-$\frac{24}{13}$,可得sinB,又角A,B,C都是锐角,可求sinA,cosB,从而由f(2C)=-2cos(A+B)=2sinAsinB-2cosAcosB即可求值.
解答 解:(1)∵f(x)=A(sin$\frac{x}{2}$cosφ+cos$\frac{x}{2}$sinφ)=Asin($\frac{x}{2}+$φ)的最大值是2,A>0,可得A=2,
∴f(0)=2sinφ=2,可得sinφ=1,φ=2k$π+\frac{π}{2}$,k∈Z,
∴由0<φ<π可解得:φ=$\frac{π}{2}$.
(2)∵由(1)可得:f(x)=2sin($\frac{x}{2}+$$\frac{π}{2}$),
∴f(2A)=2sin(A+$\frac{π}{2}$)=$\frac{6}{5}$,可得:cosA=$\frac{3}{5}$.f(2B+π)=2sin(B+π)=-2sinB=-$\frac{24}{13}$,可得:sinB=$\frac{12}{13}$,
∵角A,B,C都是锐角,可求得:sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{4}{5}$,cosB=$\sqrt{1-si{n}^{2}B}$=$\frac{5}{13}$,
∴f(2C)=2sin(C+$\frac{π}{2}$)=2cosC=-2cos(A+B)=2sinAsinB-2cosAcosB=2×$\frac{4}{5}×\frac{12}{13}$-2×$\frac{3}{5}×\frac{5}{13}$=$\frac{66}{65}$.
点评 本题主要考查了三角函数中的恒等变换应用,考查了三角形内角和定理的应用,属于基本知识的考查.

| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
 如图是一个四面体的三视图,则其外接球的体积为( )
如图是一个四面体的三视图,则其外接球的体积为( )| A. | 8$\sqrt{6}π$ | B. | $\sqrt{6}π$ | C. | 4$\sqrt{3}π$ | D. | $\sqrt{3}π$ |
 中,
中, 的对边分别是
的对边分别是 ,
, ,且
,且 .
. ,且
,且 ,求
,求 边上的中线长.
边上的中线长. 中,
中, 底面
底面 ,底面
,底面 是直角梯形,
是直角梯形, .
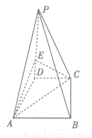
.
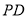 上确定一点
上确定一点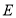 ,使得
,使得 平面
平面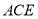 ,并求
,并求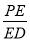 的值;
的值; 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值. 如图,在平面直角坐标系xOy中,点A(x1,y1)、B(x2,y2)在单位圆上,∠xOA=α,∠AOB=$\frac{π}{3}$,且α∈($\frac{π}{6}$,$\frac{π}{3}$).
如图,在平面直角坐标系xOy中,点A(x1,y1)、B(x2,y2)在单位圆上,∠xOA=α,∠AOB=$\frac{π}{3}$,且α∈($\frac{π}{6}$,$\frac{π}{3}$).